浙江省瑞安市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 点P(﹣1,2)在第( )象限.A、一 B、二 C、三 D、四2. 下列选项中的图标,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各组数可能是一个三角形的边长的是( )A、5,1,7 B、5,12,17 C、5,7,7 D、11,12,234. 一次函数 的图象与y轴交点坐标( )A、 B、 C、 D、5. 下列选项中,可以用来证明命题“若 ,则 ”是假命题的反例是( )A、 B、 C、 D、6. 不等式 的解集是( )A、 B、 C、 D、7. 如图,顺次连结同一平面内A,B,C,D四点,已知 , , ,若 的平分线BE经过点D,则 的度数( )
3. 下列各组数可能是一个三角形的边长的是( )A、5,1,7 B、5,12,17 C、5,7,7 D、11,12,234. 一次函数 的图象与y轴交点坐标( )A、 B、 C、 D、5. 下列选项中,可以用来证明命题“若 ,则 ”是假命题的反例是( )A、 B、 C、 D、6. 不等式 的解集是( )A、 B、 C、 D、7. 如图,顺次连结同一平面内A,B,C,D四点,已知 , , ,若 的平分线BE经过点D,则 的度数( ) A、 B、 C、 D、8. 如图所示, 的三条边长分别是a,b,c,则下列选项中的三角形与 不一定全等的是( )
A、 B、 C、 D、8. 如图所示, 的三条边长分别是a,b,c,则下列选项中的三角形与 不一定全等的是( ) A、
A、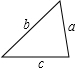 B、
B、 C、
C、 D、
D、 9. 若关于x,y的方程组 满足1<x+y<2,则k的取值范围是( )A、0<k<1 B、–1<k<0 C、1<k<2 D、0<k<10. 早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x , 两人之间的距离为y , 则下列选项中的图象能大致反映y与x之间关系的是( )A、
9. 若关于x,y的方程组 满足1<x+y<2,则k的取值范围是( )A、0<k<1 B、–1<k<0 C、1<k<2 D、0<k<10. 早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x , 两人之间的距离为y , 则下列选项中的图象能大致反映y与x之间关系的是( )A、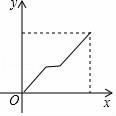 B、
B、 C、
C、 D、
D、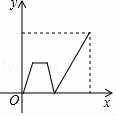
二、填空题
-
11. 用不等式表示:x与3的和大于6,则这个不等式是.12. 若直角三角形的两条直角边的长分别是3和4,则斜边上的中线长为.13. 点A(m,﹣3)向下平移3个单位后,恰好落在正比例函数y=﹣6x的图象上,则m的值为.14. 如图,在 中, ,AD平分 交BC于点D, ,则点D到AB边的距离为.
 15. 如图,在直角坐标系中,过点 分别向x轴,y轴作垂线,垂足分别为点B,C,取AC的中点P,连结OP,作点C关于直线OP的对称点D,直线PD与AB交于点Q,则线段PQ的长为 , 直线PQ的函数表达式为.
15. 如图,在直角坐标系中,过点 分别向x轴,y轴作垂线,垂足分别为点B,C,取AC的中点P,连结OP,作点C关于直线OP的对称点D,直线PD与AB交于点Q,则线段PQ的长为 , 直线PQ的函数表达式为.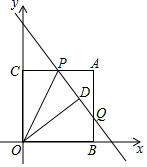 16. 如图,已知线段 ,P是AB上一动点,分别以AP,BP为斜边在AB同侧作等腰 和等腰 ,以CD为边作正方形DCFE,连结AE,BF,当 时, 为.
16. 如图,已知线段 ,P是AB上一动点,分别以AP,BP为斜边在AB同侧作等腰 和等腰 ,以CD为边作正方形DCFE,连结AE,BF,当 时, 为.
三、解答题
-
17. 解不等式组18. 已知:如图,点A、D、B、E在同一直线上, , , 求证: .
 19. 如图,在 方格中,按下列要求画三角形,使它的顶点均在方格的顶点上 小正方形的边长为
19. 如图,在 方格中,按下列要求画三角形,使它的顶点均在方格的顶点上 小正方形的边长为 (1)、在图甲中画一个面积为6的等腰三角形;(2)、在图乙中画一个三角形与 全等,且有一条公共边.20. 如图,在直角坐标系中,直线 分别交x轴,y轴于点E,F,交直线 于点P,过线段OP上点A作x轴,y轴的平行线分别交y轴于点C,直线EF于点B.
(1)、在图甲中画一个面积为6的等腰三角形;(2)、在图乙中画一个三角形与 全等,且有一条公共边.20. 如图,在直角坐标系中,直线 分别交x轴,y轴于点E,F,交直线 于点P,过线段OP上点A作x轴,y轴的平行线分别交y轴于点C,直线EF于点B. (1)、求点P的坐标.(2)、当 时,求点P到线段AB的距离.21. 如图,在 与 中, , , ,连结CA,BD.
(1)、求点P的坐标.(2)、当 时,求点P到线段AB的距离.21. 如图,在 与 中, , , ,连结CA,BD. (1)、求证: ≌ ;(2)、连接BC,若 , ,
(1)、求证: ≌ ;(2)、连接BC,若 , ,判断 的形状.
求 的度数.
22. 为了响应“足球进校园”的号召,学校开设了足球兴趣拓展班,计划同时购买A,B两种足球30个,A,B两种足球的价格分别为50元 个,80元 个,设购买B种足球x个,购买两种足球的总费用为y元.(1)、求y关于x的函数表达式.(2)、在总费用不超过1600元的前提下,从节省费用的角度来考虑,求总费用的最小值.(3)、因足球兴趣拓展班的人数增多,所以实际购买中这两种足球总数超过30个,总费用为2000元,则该学校可能共购买足球个 直接写出答案23. 如图,在直角坐标系中,直线 与x轴正半轴,y轴正半轴分别交于点A,B,点 ,点E在第一象限, 为等边三角形,连接AE,BE (1)、求点E的坐标;(2)、当BE所在的直线将 的面积分为3:1时,求 的面积;(3)、取线段AB的中点P,连接PE,OP,当 是以OE为腰的等腰三角形时,则 直接写出b的值
(1)、求点E的坐标;(2)、当BE所在的直线将 的面积分为3:1时,求 的面积;(3)、取线段AB的中点P,连接PE,OP,当 是以OE为腰的等腰三角形时,则 直接写出b的值