浙江省宁波市鄞州区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 满足不等式 $x > 2$ 的正整数是（）

A、2.5 B、 $\sqrt{5}$ C、-2 D、5

查看试题解析
2. 下列标志中，可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在平面直角坐标系中，点 $P (- 2018, 2019)$ 的位置所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 若 $x > y$ ，且 $(a - 3) x < (a - 3) y$ ，则 $a$ 的值可能是（）

A、0 B、3 C、4 D、5

查看试题解析
5. $Δ A B C$ 的内角分别为 $∠ A, ∠ B, ∠ C$ ，下列能判定 $Δ A B C$ 是直角三角形的条件是（）

A、 $∠ A = 2 ∠ B = 3 ∠ C$ B、 $∠ C = 2 ∠ B$ C、 $∠ A : ∠ B : ∠ C = 3 : 4 : 5$ D、 $∠ A + ∠ B = ∠ C$

查看试题解析
6. 如图，已知 $∠ A B C = ∠ D C B$ ，添加以下条件，不能判定 $Δ A B C ≌ Δ D C B$ 的是（）

A、 $∠ A = ∠ D$ B、 $∠ A C B = ∠ D B C$ C、 $A C = D B$ D、 $A B = D C$

查看试题解析
7. 如图， $B P$ 平分 $∠ A B C$ ， $D$ 为 $B P$ 上一点， $E ， F$ 分别在 $B A ， B C$ 上，且满足 $D E = D F$ ，若 $∠ B E D = 140^{°}$ ，则 $∠ B F D$ 的度数是（）

A、40° B、50° C、60° D、70°

查看试题解析
8. 要说明命题“若 $a > b$ ，则 $a^{2} > b^{2}$ ”是假命题，能举的一个反例是（）

A、 $a = 3 ， b = 2$ B、 $a = 4 ， b = - 1$ C、 $a = 1 ， b = 0$ D、 $a = 1 ， b = - 2$

查看试题解析
9. 直线 $y = k x$ 过点 $A (m, n)$ ， $B (m - 3, n + 4)$ ，则 $k$ 的值是（）

A、 $\frac{4}{3}$ B、 $- \frac{4}{3}$ C、 $\frac{3}{4}$ D、 $- \frac{3}{4}$

查看试题解析
10. 如图，在 $Δ A B C$ 中，点 $D$ 是 $B C$ 边上一点， $A D = A C$ ，过点 $D$ 作 $D E ⊥ B C$ 交 $A B$ 于 $E$ ，若 $Δ A D E$ 是等腰三角形，则下列判断中正确的是（）

A、 $∠ B = ∠ C A D$ B、 $∠ B E D = ∠ C A D$ C、 $∠ A D B = ∠ A E D$ D、 $∠ B E D = ∠ A D C$

查看试题解析

二、填空题

11. 函数 $y = \frac{1}{x - 5}$ 中，自变量 $x$ 的取值范围是.

查看试题解析
12. 点 $P (- 2, 9)$ 与点 $Q$ 关于 $x$ 轴对称，则点 $Q$ 的坐标是.

查看试题解析
13. 根据数量关系： $x$ 的5倍加上1是正数，可列出不等式：.

查看试题解析
14. 如图，将三角形纸片（ $Δ A B C$ ）进行折叠，使得点 $B$ 与点 $A$ 重合，点 $C$ 与点 $A$ 重合，压平出现折痕 $D E ， F G$ ，其中 $D ， F$ 分别在边 $A B ， A C$ 上， $E ， G$ 在边 $B C$ 上，若 $∠ B = 25 °$ ， $∠ C = 45 °$ ，则 $∠ E A G$ 的度数是.

查看试题解析
15. 已知点 $P$ 是直线 $y = - 2 x + 4$ 上的一个动点，若点 $P$ 到两坐标轴的距离相等，则点 $P$ 的坐标是.

查看试题解析
16. 如图， $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 60 °$ ， $A B = 4$ ，点 $D$ 是 $B C$ 上一动点，以 $B D$ 为边在 $B C$ 的右侧作等边 $Δ B D E$ ， $F$ 是 $D E$ 的中点，连结 $A F ， C F$ ，则 $A F + C F$ 的最小值是.

查看试题解析

三、解答题

17. 解不等式组 $\{\begin{cases} x - 1 \leq 2 \\ \frac{x + 1}{2} \geq \frac{x + 1}{3} \end{cases}$ ，并写出不等式组的整数解.

查看试题解析
18. 已知：如图，在 $Δ A B C$ 中， AD⊥BC 于点 $D$ ， $E$ 为AC上一点，连结 BE 交 AD 于 $F$ ，且 $A C = B F$ ，DC=DF，求证： BE⊥AC .

查看试题解析
19. 一次函数 y=kx+b 的图像经过A（3，2），B(1，6）两点.

(1)、求 k，b 的值；

(2)、判断点 P（-1，10）是否在该函数的图象上.

查看试题解析
20. 如图是由25个边长为1的小正方形组成的 5×5 网格，请在图中画出以 $D E$ 为斜边的2个面积不同的直角三角形.（要求：所画三角形顶点都在格点上）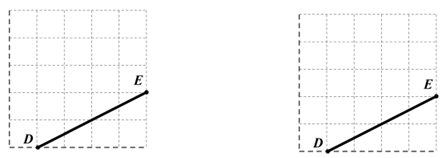

查看试题解析
21. 某小区积极创建环保示范社区，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，已知温馨提示牌的单价为每个30元，垃圾箱的单价为每个90元，共需购买温馨提示牌和垃圾箱共100个.

(1)、若规定温馨提示牌和垃圾箱的个数之比为1:4，求所需的购买费用；

(2)、若该小区至多安放48个温馨提示牌，且费用不超过6300元，请列举所有购买方案，并说明理由.

查看试题解析
22. 某市推出电脑上网包月制，每月收取费用y（元）与上网时间x（小时）的函数关系如图所示，其中BA是线段，且BA∥x轴，AC是射线.

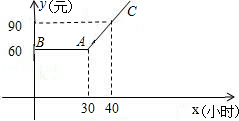(1)、当x≥30，求y与x之间的函数关系式；

(2)、若小李4月份上网20小时，他应付多少元的上网费用？

(3)、若小李5月份上网费用为75元，则他在该月份的上网时间是多少？

查看试题解析
23. 如图1， $Δ A B C$ 的 $∠ A ， ∠ B ， ∠ C$ 所对边分别是 $a ， b ， c$ ，且 $a \leq b \leq c$ ，若满足a²+c²=2b² ，则称 $Δ A B C$ 为奇异三角形，例如等边三角形就是奇异三角形.

(1)、若 a=2，b= $\sqrt{10}$ ， c=4 ，判断 $Δ A B C$ 是否为奇异三角形，并说明理由；

(2)、若∠C=90° ， $c = 3$ ，求 b 的长；

(3)、如图2，在奇异三角形 $Δ A B C$ 中， $b = 2$ ，点 $D$ 是AC 边上的中点，连结 BD ， BD 将 $Δ A B C$ 分割成2个三角形，其中 △ADB 是奇异三角形，△BCD 是以CD为底的等腰三角形，求 c 的长.

查看试题解析
24. 如图，在平面直角坐标系中， $A (3 ， 0)$ ， $B (0 ， 3)$ ，过点B 画y轴的垂线 l ，点 C 在线段AB 上，连结 OC 并延长交直线 l 于点 D ，过点 C 画 CE⊥OC 交直线 l 于点 E .

(1)、求 ∠OBA 的度数，并直接写出直线AB的解析式；

(2)、若点C的横坐标为2，求BE的长；

(3)、当 BE=1 时，求点C的坐标.

查看试题解析