浙江省宁波市海曙区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 若点P的坐标是(2,1),则点P在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 以下图形中对称轴的数量小于3的是( )A、
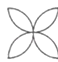 B、
B、 C、
C、 D、
D、 3. 若三角形的三边长分别为3,4,x , 则x的值可能是( )A、1 B、6 C、7 D、104. 下列说法中:①法国数学家笛卡尔首先建立了坐标思想;②全等三角形对应边上的中线长相等;③若 则 ④有两边和其中一条边所对的一个角对应相等的两个三角形一定全等.说法正确的为( )A、①③④ B、②④ C、①② D、②③④5. 下列函数中, 是 的一次函数是( )A、①②③ B、①③④ C、①②③④ D、②③④6.
3. 若三角形的三边长分别为3,4,x , 则x的值可能是( )A、1 B、6 C、7 D、104. 下列说法中:①法国数学家笛卡尔首先建立了坐标思想;②全等三角形对应边上的中线长相等;③若 则 ④有两边和其中一条边所对的一个角对应相等的两个三角形一定全等.说法正确的为( )A、①③④ B、②④ C、①② D、②③④5. 下列函数中, 是 的一次函数是( )A、①②③ B、①③④ C、①②③④ D、②③④6.如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )
 A、∠D=∠C B、BD=AC C、∠CAD=∠DBC D、AD=BC7. 不等式组 的解集在数轴上表示为( )
A、∠D=∠C B、BD=AC C、∠CAD=∠DBC D、AD=BC7. 不等式组 的解集在数轴上表示为( )
A、 B、
B、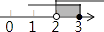 C、
C、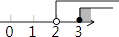 D、
D、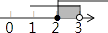 8. 已知下列命题:①若 则 ②若 则 ③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )A、1 B、2 C、3 D、49. 等腰 的周长为 ,则其腰长 的取值范围是( ).A、 B、 C、 D、10. 图象中所反应的过程是:小敏从家跑步去体育馆,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中 表示时间, 表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
8. 已知下列命题:①若 则 ②若 则 ③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )A、1 B、2 C、3 D、49. 等腰 的周长为 ,则其腰长 的取值范围是( ).A、 B、 C、 D、10. 图象中所反应的过程是:小敏从家跑步去体育馆,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中 表示时间, 表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( ) A、体育场离小敏家2.5千米 B、体育场离早餐店4千米 C、小敏在体育场锻炼了15分钟 D、小敏从早餐店回到家用时30分钟
A、体育场离小敏家2.5千米 B、体育场离早餐店4千米 C、小敏在体育场锻炼了15分钟 D、小敏从早餐店回到家用时30分钟二、填空题
-
11. 若函数y=2x+b(b为常数)的图象经过点A(0,﹣2),则b= .12. 已知点P(-2,3)关于y轴的对称点为Q(a,b),则a+b的值是.13. 已知一个等腰三角形两内角的度数之比为1∶4,则这个等腰三角形顶角的度数为 .14. 若不等式组 的解集是-1<x<2,则 .
15. 将直线 向右平移2个单位后得到直线 则直线 的解析式是.16. 一次数学知识竞赛中,竞赛题共30题,规定:答对一道题得4分,不答或答错一道题倒扣2分,若得分不低于60分者获奖,则获奖者至少答对道题.17. 为节约用水,某市居民生活用水按级收费,具体收费标准如下表:用水量(吨)
不超过17吨的部分
超过17吨不超过31吨的部分
超过31吨的部分
单位(元/吨)
3
5
7
设某户居民家的月用水量为 吨,应付水费为 元,则 关于 的函数表达式为.
18. 有一组平行线 过点A作AM⊥ 于点M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线 于点C,在直线 上取点B使BM=CN,若直线 与 间的距离为2, 与 间的距离为4,则BC=.
三、解答题
-
19. 如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
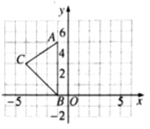 (1)、请画出△ABC关于y轴对称的△A’B’C’(其中A’,B’,C’分別是A,B,C的对应点,不写画法);(2)、直接写出A’,B’,C’三点的坐标:A’(),B’(),C’();20. 如图,在 中,AE是 的角平分线,AD是BC边上的高,且 , ,求 、 的度数.
(1)、请画出△ABC关于y轴对称的△A’B’C’(其中A’,B’,C’分別是A,B,C的对应点,不写画法);(2)、直接写出A’,B’,C’三点的坐标:A’(),B’(),C’();20. 如图,在 中,AE是 的角平分线,AD是BC边上的高,且 , ,求 、 的度数. 21. 已知直线y=kx+b经过点A(5,0),B(1,4).
21. 已知直线y=kx+b经过点A(5,0),B(1,4). (1)、求直线AB的函数表达式;(2)、若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.22. 如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0<∠ACF<45°.
(1)、求直线AB的函数表达式;(2)、若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.22. 如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0<∠ACF<45°. (1)、求证:△BEC≌△CFA;(2)、若AF=5,EF=8,求BE的长.
(1)、求证:△BEC≌△CFA;(2)、若AF=5,EF=8,求BE的长.
