浙江省丽水市庆元县2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期：2019-08-05 类型：期末考试
一、单选题
-
1. 下列各点中在第四象限的是（ ）A、 B、 C、 D、2. 若三角形的两边长为2和3，则第三边长可以是（ ）A、1 B、3 C、5 D、73. 不等式x≥-1的解在数轴上表示为（ ）A、
B、
C、
D、
4. 下列命题中是假命题的是（ ）A、同位角相等，两直线平行 B、等腰三角形底边上的高线和中线相互重合 C、等腰三角形的两个底角相等 D、周长相等的两个三角形全等5. 如图，已知OD=OE，那么添加下列条件后，仍无法判定△OBD≌△OCE的是（ ）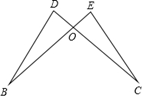
A、 B、 C、 D、6. 直角坐标系中，点P(2，﹣4)先向右平移4个单位后的坐标是（ ）A、(2，0) B、(2，﹣8) C、(6，﹣4) D、(﹣2，﹣4)7. 不等式组 的解集是（ ）A、 B、 C、 D、无解8. 已知点A(k，10)在直线y=kx+1上，且y随x的增大而减小，则k的值为（ ）A、3 B、 C、 D、9. 庆元大道两侧需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率，该绿化组完成的绿化面积S(单位m2)与工作时间t(单位：h)之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是（ ）
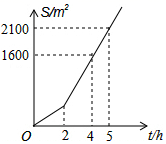A、200 B、300 C、400 D、50010. 如图，在等腰直角△ABC中，腰长AB=4，点D在CA的延长线上，∠BDA=30°，则△ABD的面积是（ ）
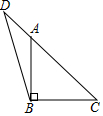A、 B、 C、 D、二、填空题
-
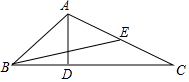
11. 点(1，-3)关于y轴的对称点坐标是.12. 函数y=-x+4经过的象限是.13. 如图，在△ABC中，AB=AD=DC，∠B=70°，则∠C=.
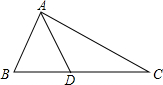14. 用不等式表示“x的2倍与3的和大于10”是.15. 直角三角形两直角边长分别为3和4，则它斜边上的高为 ．16. 如图，以矩形ABCD的相邻边建立直角坐标系，AB=3，BC=5.点E是边CD上一点，将△ADE沿着AE翻折，点D恰好落在BC边上，记为F.
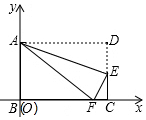(1)、求折痕AE所在直线的函数解析式；(2)、若把翻折后的矩形沿y轴正半轴向上平移m个单位，连结OF，若△OAF是等腰三角形，则m的值是 ，三、解答题
-
17. 解不等式：3x＞2(x-1)+218. 如图，在8×8的方格纸中，△ABC是格点三角形，且A(-2，4)，C(0，3).
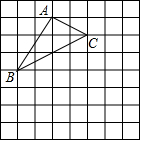(1)、在8×8的方格纸中建立平面直角坐标系，并求出B点坐标；(2)、求△ABC的面积.19. 已知∠O及其两边上点A和B(如图)，用直尺和圆规作一点P，使点P到∠O的两边距离相等，且到点A，B的距离也相等.(保留作图痕迹)
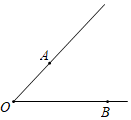20. 如图，一次函数y=kx+b图象经过(1，6)，(-1，2)
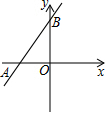(1)、求k，b的值；(2)、若y＞0，求x的取值范围.21. 已知，如图，Rt△ABC中，∠BAC=90°，AB=AC，点D是BC上任意一点，过B作BE⊥AD于点E，过C作CF⊥AD于点F.求证：BE=CF+EF.
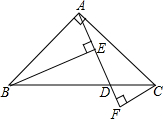22. 如图，正方形ABCD的边长为6cm，动点P从A点出发，在正方形的边上由A→B→C→D运动，设运动的时间为t(s)，△APD的面积为S(cm2)，S与t的函数图象如图所示
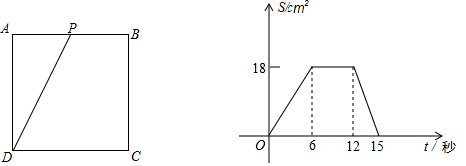(1)、求点P在BC上运动的时间范围；(2)、当t为何值时，△APD的面积为10cm2.
