浙江省杭州市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组数不可能是一个三角形的边长的是A、5,5,5 B、5,7,7 C、5,12,13 D、5,7,123. 一次函数 的图象经过的象限是( )A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限4. 用不等式表示“ 的一半不小于-7”,正确的是( )A、 B、 C、 D、5. 已知 是直角坐标系中任意位置的一个三角形,现将 各顶点的纵坐标乘以 ,得到 ,则它与 的位置关系是( )A、关于x轴对称 B、关于y轴对称 C、关于直线 对称 D、关于直线 对称6. 已知 ,则下列变形正确的是( )A、 B、若 ,则 C、 D、若 ,则7. 在国内投寄平信应付邮资如下表:
2. 下列各组数不可能是一个三角形的边长的是A、5,5,5 B、5,7,7 C、5,12,13 D、5,7,123. 一次函数 的图象经过的象限是( )A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限4. 用不等式表示“ 的一半不小于-7”,正确的是( )A、 B、 C、 D、5. 已知 是直角坐标系中任意位置的一个三角形,现将 各顶点的纵坐标乘以 ,得到 ,则它与 的位置关系是( )A、关于x轴对称 B、关于y轴对称 C、关于直线 对称 D、关于直线 对称6. 已知 ,则下列变形正确的是( )A、 B、若 ,则 C、 D、若 ,则7. 在国内投寄平信应付邮资如下表:信件质量 克
邮资 元 封
则y关于x的函数图象正确的是( )
A、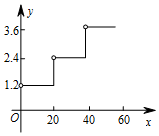 B、
B、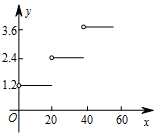 C、
C、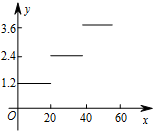 D、
D、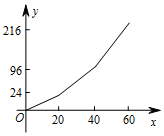 8. 如图,已知直线 和直线 交于点 ,则关于x的不等式 的解是( )
8. 如图,已知直线 和直线 交于点 ,则关于x的不等式 的解是( )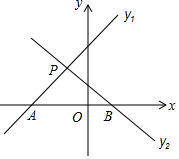 A、 B、 C、 D、9. 给出下列命题: 两边及一边上的中线对应相等的两个三角形全等; 底边和顶角对应相等的两个等腰三角形全等; 斜边和斜边上的高线对应相等的两个直角三角形全等,其中属于真命题的是( )A、 B、 C、 D、10. 如图,射线 射线CD, 与 的平分线交于点E, ,点P是射线AB上的一动点,连结PE并延长交射线CD于点 给出下列结论: 是直角三角形; ; 设 , ,则y关于x的函数表达式是 ,其中正确的是( )
A、 B、 C、 D、9. 给出下列命题: 两边及一边上的中线对应相等的两个三角形全等; 底边和顶角对应相等的两个等腰三角形全等; 斜边和斜边上的高线对应相等的两个直角三角形全等,其中属于真命题的是( )A、 B、 C、 D、10. 如图,射线 射线CD, 与 的平分线交于点E, ,点P是射线AB上的一动点,连结PE并延长交射线CD于点 给出下列结论: 是直角三角形; ; 设 , ,则y关于x的函数表达式是 ,其中正确的是( )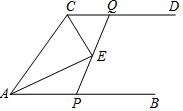 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知正比例函数 ,则当 时, .12. 已知等腰三角形的一个内角是 ,则其余两个角的度数分别是度,度13. 如图,AD是 的中线, ,把 沿着直线AD对折,点C落在点E的位置,如果 ,那么线段BE的长度为.
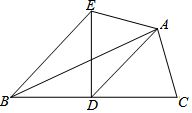 14. 已知点 是直线 上的点,且到 轴的距离等于 ,则点 的坐标为.15. 已知 ,且 .(1)、x的取值范围是;(2)、若设 ,则m的最大值是.16. 在 中, ,边AB的垂直平分线交边BC于点D,边AC的垂直平分线交边BC于点E,连结AD,AE,则 的度数为 用含 的代数式表示
14. 已知点 是直线 上的点,且到 轴的距离等于 ,则点 的坐标为.15. 已知 ,且 .(1)、x的取值范围是;(2)、若设 ,则m的最大值是.16. 在 中, ,边AB的垂直平分线交边BC于点D,边AC的垂直平分线交边BC于点E,连结AD,AE,则 的度数为 用含 的代数式表示三、解答题
-
17. 解不等式组 ,并求其整数解.18. 如图,已知线段a,b和 ,用直尺和圆规作 ,使 , , 不写作法,保留作图痕迹
 19. 如图,在△ 中,点 , 分别在边 , 上, 与 交于点 ,给出下列三个条件:① ;② ;③ .
19. 如图,在△ 中,点 , 分别在边 , 上, 与 交于点 ,给出下列三个条件:① ;② ;③ . (1)、上述三个条件中,由哪两个条件可以判定△ 是等腰三角形?(用序号写出所有成立的情形)(2)、请选择(1)中的一种情形,写出证明过程.20. 如图,把△ABC平移,使点A平移到点O.
(1)、上述三个条件中,由哪两个条件可以判定△ 是等腰三角形?(用序号写出所有成立的情形)(2)、请选择(1)中的一种情形,写出证明过程.20. 如图,把△ABC平移,使点A平移到点O.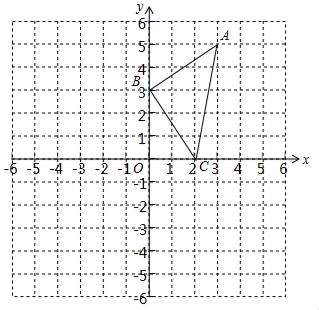 (1)、作出平移后的△OB'C';(2)、写出△OB'C'的顶点坐标,并描述这个平移过程.21. 已知 中, , , .(1)、求证: 是直角三角形;(2)、当 时,求m,n满足的关系式.
(1)、作出平移后的△OB'C';(2)、写出△OB'C'的顶点坐标,并描述这个平移过程.21. 已知 中, , , .(1)、求证: 是直角三角形;(2)、当 时,求m,n满足的关系式.
