广西柳州市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-08-05 类型:期末考试
一、单选题
-
1. 计算a•a3=( )A、a B、a3 C、a4 D、2a2. 若分式 有意义,则 应满足的条件是( ).A、 B、 C、 D、3. 若一个三角形的两边长分别为3和7,则第三边长可能是( )A、6 B、3 C、2 D、114. 如图,x=( )
 A、65 B、75 C、85 D、955. 如图,∠1=125°,∠C=65°,则∠A=( )
A、65 B、75 C、85 D、955. 如图,∠1=125°,∠C=65°,则∠A=( )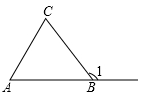 A、125° B、65° C、70° D、60°6. 化简 的结果为( )A、 B、a﹣1 C、a D、17. 如图,已知AB=AC,AD=AE,若添加一个条件不能得到“△ABD≌△ACE”是( )
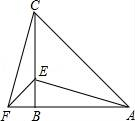
A、125° B、65° C、70° D、60°6. 化简 的结果为( )A、 B、a﹣1 C、a D、17. 如图,已知AB=AC,AD=AE,若添加一个条件不能得到“△ABD≌△ACE”是( )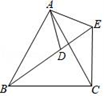 A、∠ABD=∠ACE B、BD=CE C、∠BAD=∠CAE D、∠BAC=∠DAE8. 下列从左到右的变形属于因式分解的是( )A、2a(a+1)=2a2+2a B、a2﹣6a+9=a(a﹣6)+9 C、a2+3a+2=(a+1)(a+2) D、a2﹣1=a(a﹣ )9. 某厂进行技术创新,现在每天比原来多生产30台机器,并且现在生产500台机器所需时间与原来生产350台机器所需时间相同.设现在每天生产x台机器,根据题意可得方程为( )A、 B、 C、 D、10. 如图所示,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC.下列结论一定成立的是( )
A、∠ABD=∠ACE B、BD=CE C、∠BAD=∠CAE D、∠BAC=∠DAE8. 下列从左到右的变形属于因式分解的是( )A、2a(a+1)=2a2+2a B、a2﹣6a+9=a(a﹣6)+9 C、a2+3a+2=(a+1)(a+2) D、a2﹣1=a(a﹣ )9. 某厂进行技术创新,现在每天比原来多生产30台机器,并且现在生产500台机器所需时间与原来生产350台机器所需时间相同.设现在每天生产x台机器,根据题意可得方程为( )A、 B、 C、 D、10. 如图所示,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC.下列结论一定成立的是( ) A、AB=BF B、AE=ED C、AD=DC D、∠ABE=∠DFE
A、AB=BF B、AE=ED C、AD=DC D、∠ABE=∠DFE二、填空题
-
11. 将数字0.0026用科学记数法表示为.12. 当x=时,分式 的值为0.13. 已知△ABC的三个内角分别是∠A.∠B、∠C,若∠A=60°,∠C=2∠B,则∠C=14. 一个多边形的内角和是它的外角和的3倍,则这个多边形的边数为 .15. 如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若∠CAE=32°,则∠ACF的度数为°.
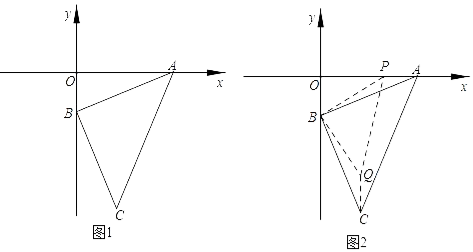
 16. 如图,在△ABC中,∠ABC=60°,BC=2,CD是△ABC的一条高线.若E,F分别是CD和BC上的动点,则BE+EF的最小值是.
16. 如图,在△ABC中,∠ABC=60°,BC=2,CD是△ABC的一条高线.若E,F分别是CD和BC上的动点,则BE+EF的最小值是.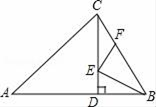
三、解答题
-
17. 计算:(4a+1)(a+2)﹣(2a+1)(a﹣1).18. 分解因式:8a3﹣8a2+2a.19. 解分式方程: .20. 如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A'重合.
 (1)、若∠B=50°,∠C=60°,求∠A的度数;(2)、若∠1+∠2=130°,求∠A的度数.21. 如图,AB∥CD,∠A=90°,E是AD边的中点,CE平分∠BCD.
(1)、若∠B=50°,∠C=60°,求∠A的度数;(2)、若∠1+∠2=130°,求∠A的度数.21. 如图,AB∥CD,∠A=90°,E是AD边的中点,CE平分∠BCD.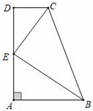 (1)、求证:BE平分∠ABC;(2)、若AB=2,CD=1,求BC的长.
(1)、求证:BE平分∠ABC;(2)、若AB=2,CD=1,求BC的长.