2017年山东省滨州市中考数学试卷

试卷更新日期：2017-06-16 类型：中考真卷

进入出卷网下载

一、选择题（本大题共12个小题，在每小题的四个选项中只有一个是正确的，请把正确的选项选出来，用2B铅笔把答题卡上对应题目的答案标号涂黑，每小题涂对得3分，满分36分）

1. 计算﹣（﹣1）+|﹣1|，其结果为（）

A、﹣2 B、2 C、0 D、﹣1

查看试题解析
2. 一元二次方程x²﹣2x=0根的判别式的值为（）

A、4 B、2 C、0 D、﹣4

查看试题解析
3. 如图，直线AC∥BD，AO、BO分别是∠BAC、∠ABD的平分线，那么下列结论错误的是（）

A、∠BAO与∠CAO相等 B、∠BAC与∠ABD互补 C、∠BAO与∠ABO互余 D、∠ABO与∠DBO不等

查看试题解析
4. 下列计算：（1） ${(\sqrt{2})}^{2}$ =2，（2） $\sqrt{{(- 2)}^{2}}$ =2，（3）（﹣2 $\sqrt{3}$ ）²=12，（4）（ $\sqrt{2}$ + $\sqrt{3}$ ）（ $\sqrt{2}$ ﹣ $\sqrt{3}$ ）=﹣1，其中结果正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 若正方形的外接圆半径为2，则其内切圆半径为（）

A、 $\sqrt{2}$ B、2 $\sqrt{2}$ C、 $\frac{\sqrt{2}}{2}$ D、1

查看试题解析
6. 分式方程 $\frac{x}{x - 1}$ ﹣1= $\frac{3}{(x - 1) (x + 2)}$ 的解为（）

A、x=1 B、x=﹣1 C、无解 D、x=﹣2

查看试题解析
7. 如图，在△ABC中，AC⊥BC，∠ABC=30°，点D是CB延长线上的一点，且BD=BA，则tan∠DAC的值为（）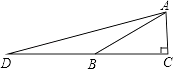

A、2+ $\sqrt{3}$ B、2 $\sqrt{3}$ C、3+ $\sqrt{3}$ D、3 $\sqrt{3}$

查看试题解析
8. 如图，在△ABC中，AB=AC，D为BC上一点，且DA=DC，BD=BA，则∠B的大小为（）

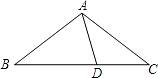A、40° B、36° C、30° D、25°

查看试题解析
9. 某车间有27名工人，生产某种由一个螺栓套两个螺母的产品，每人每天生产螺母16个或螺栓22个，若分配x名工人生产螺栓，其他工人生产螺母，恰好使每天生产的螺栓和螺母配套，则下面所列方程中正确的是（）

A、22x=16（27﹣x） B、16x=22（27﹣x） C、2×16x=22（27﹣x） D、2×22x=16（27﹣x）

查看试题解析
10. 若点M（﹣7，m）、N（﹣8，n）都在函数y=﹣（k²+2k+4）x+1（k为常数）的图象上，则m和n的大小关系是（）

A、m＞n B、m＜n C、m=n D、不能确定

查看试题解析
11. 如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（）

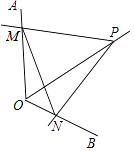A、4 B、3 C、2 D、1

查看试题解析
12. 在平面直角坐标系内，直线AB垂直于x轴于点C（点C在原点的右侧），并分别与直线y=x和双曲线y= $\frac{1}{x}$ 相交于点A、B，且AC+BC=4，则△OAB的面积为（）

A、2 $\sqrt{3}$ +3或2 $\sqrt{3}$ ﹣3 B、 $\sqrt{2}$ +1或 $\sqrt{2}$ ﹣1 C、2 $\sqrt{3}$ ﹣3 D、 $\sqrt{2}$ ﹣1

查看试题解析

二、填空题：本大题共6个小题，每小题4分，满分24分

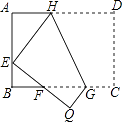
13. 计算： $\frac{3}{\sqrt{3}}$ +（ $\sqrt{3}$ ﹣3）⁰﹣|﹣ $\sqrt{12}$ |﹣2^﹣1﹣cos60°= ．

查看试题解析
14. 不等式组 ${\begin{matrix} x - 3 (x - 2) > 4 \\ \frac{2 x - 1}{5} \leq \frac{x + 1}{2} \end{matrix}$ 的解集为．

查看试题解析
15. 在平面直角坐标系中，点C、D的坐标分别为C（2，3）、D（1，0），现以原点为位似中心，将线段CD放大得到线段AB．若点D的对应点B在x轴上且OB=2，则点C的对应点A的坐标为．

查看试题解析
16. 如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在AB边上的E处，EQ与BC相交于点F，若AD=8，AE=4，则△EBF周长的大小为．

查看试题解析
17. 如图，一个几何体的三视图分别是两个矩形，一个扇形，则这个几何体表面积的大小为．

查看试题解析
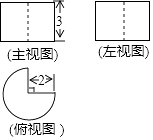18. 观察下列各式： $\frac{2}{1 \times 3}$ = $\frac{1}{1}$ ﹣ $\frac{1}{3}$ ；
$\frac{2}{2 \times 4}$ = $\frac{1}{2}$ ﹣ $\frac{1}{4}$ ；

$\frac{2}{3 \times 5}$ = $\frac{1}{3}$ ﹣ $\frac{1}{5}$ ；

…

请利用你所得结论，化简代数式： $\frac{1}{1 \times 3}$ + $\frac{1}{2 \times 4}$ + $\frac{1}{3 \times 5}$ +…+ $\frac{1}{n (n + 2)}$ （n≥3且n为整数），其结果为．

查看试题解析

三、解答题（共6小题，满分60分）

19. （Ⅰ）计算：（a﹣b）（a²+ab+b²）
（Ⅱ）利用所学知识以及（Ⅰ）所得等式，化简代数式 $\frac{m^{3} - n^{3}}{m^{2} + m n + n^{2}}$ ÷ $\frac{m^{2} - n^{2}}{m^{2} + 2 m n + n^{2}}$ ．

查看试题解析
20. 根据要求，解答下列问题：

(1)、解答下列问题
①方程x²﹣2x+1=0的解为；
②方程x²﹣3x+2=0的解为；
③方程x²﹣4x+3=0的解为；
…

(2)、根据以上方程特征及其解的特征，请猜想：
①方程x²﹣9x+8=0的解为；
②关于x的方程的解为x₁=1，x₂=n．

(3)、请用配方法解方程x²﹣9x+8=0，以验证猜想结论的正确性．

查看试题解析
21. 为了考察甲、乙两种成熟期小麦的株高长势情况，现从中随机抽取6株，并测得它们的株高（单位：cm）如下表所示：
甲
63
66
63
61
64
61
乙
63
65
60
63
64
63
（Ⅰ）请分别计算表内两组数据的方差，并借此比较哪种小麦的株高长势比较整齐？
（Ⅱ）现将进行两种小麦优良品种杂交实验，需从表内的甲、乙两种小麦中，各随机抽取一株进行配对，以预估整体配对情况，请你用列表法或画树状图的方法，求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率．

查看试题解析
22. 如图，在▱ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于 $\frac{1}{2}$ BF的相同长为半径画弧，两弧交于点P；连接AP并延长交BC于点E，连接EF，则所得四边形ABEF是菱形．
（Ⅰ）根据以上尺规作图的过程，求证：四边形ABEF是菱形；
（Ⅱ）若菱形ABEF的周长为16，AE=4 $\sqrt{3}$ ，求∠C的大小．

查看试题解析
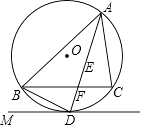
23. 如图，点E是△ABC的内心，AE的延长线交BC于点F，交△ABC的外接圆⊙O于点D，连接BD，过点D作直线DM，使∠BDM=∠DAC．
（Ⅰ）求证：直线DM是⊙O的切线；
（Ⅱ）求证：DE²=DF•DA．

查看试题解析
24.
如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛物线y=﹣x²+2x+1与y轴交于点C．
（Ⅰ）求直线y=kx+b的函数解析式；
（Ⅱ）若点P（x，y）是抛物线y=﹣x²+2x+1上的任意一点，设点P到直线AB的距离为d，求d关于x的函数解析式，并求d取最小值时点P的坐标；
（Ⅲ）若点E在抛物线y=﹣x²+2x+1的对称轴上移动，点F在直线AB上移动，求CE+EF的最小值．

查看试题解析

甲	63	66	63	61	64	61
乙	63	65	60	63	64	63