安徽省黄山市2019届高中毕业班理数第三次质量检测试卷

试卷更新日期：2019-08-02 类型：高考模拟

进入出卷网下载

一、选择题（本大题共12小题，每小题5分，共60分。）

1. 已知复数 $\frac{a + 3 i}{1 - 2 i}$ 是纯虚数，则实数a为（）

A、-6 B、6 C、 $- \frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
2. 集合A={x|2lgx<1}，B={x|x²-9≤0}，则A∩B=（）

A、[-3，3] B、（0， $\sqrt{10}$ ） C、（0.3] D、[-3， $\sqrt{10}$ ）

查看试题解析

3. 为了判断高中生选修理科是否与性别有关，现随机抽取50名学生，得到如下2×2列联表：

	理科	文科	合计
男	13	10	23
女	7	20	27
合计	20	30	50

根据表中数据，得到K²的观测值k= $\frac{50 \times {(13 \times 20 - 10 \times 7)}^{2}}{23 \times 27 \times 20 \times 30}$ ≈4.844，若已知P（K²≥3.841）≈0.05，P（K²≥5.024）~0.025，则认为选修理科与性别有关系出错的可能性约为（）

A、25% B、5% C、1% D、10%

查看试题解析

4. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （a>0，b>0）的离心率为 $\frac{\sqrt{7}}{2}$ ，且它的一个焦点到渐近线的距离为 $\sqrt{3}$ ，则该双曲线的方程为（）

A、 $\frac{x^{2}}{12} - \frac{y^{2}}{9} = 1$ B、 $\frac{x^{2}}{28} - \frac{y^{2}}{21} = 1$ C、 $\frac{x^{2}}{16} - \frac{y^{2}}{12} = 1$ D、 $\frac{x^{2}}{4} - \frac{y^{2}}{3} = 1$

查看试题解析
5. 执行如图所示的程序框图，若输出s=4，则判断框内应填入的条件是（）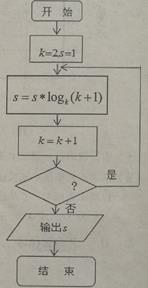

A、k≤14 B、k≤15 C、k≤16 D、k<17

查看试题解析
6. 已知（1+x）（1-ax）⁵的展开式中x²的系数为 $- \frac{5}{8}$ ，则a=（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
7. 谢尔宾斯基三角形（Sierpinski triangle）是一种分形，由波兰数学家谢尔宾斯基在1915年提出.在一个正三角形中，挖去一个“中心三角形”（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个“中心三角形”，我们用白色三角形代表挖去的部分，黑色三角形为剩下的部分，我们称此三角形为谢尔宾斯基三角形.若在图（3）内随机取一点，则此点取自谢尔宾斯基三角形的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{9}{16}$ D、 $\frac{5}{16}$

查看试题解析
8. 将函数g（x）=4cos²（ $\frac{x}{2} + \frac{π}{6}$ ）-2的图象向右平移 $\frac{π}{2}$ 个单位长度，再把横坐标缩短到原来的 $\frac{1}{2}$ 倍（纵坐标不变）得到函数f（x）的图象，则下列说法正确的是（）

A、函数f（x）的最小正周期为2π B、函数f（x）在区间[ $\frac{7 π}{12}$ ， $\frac{5 π}{4}$ ]上单调递增 C、函数f（x）在区间[ $\frac{2 π}{3}$ ， $\frac{5 π}{4}$ ]上的最小值为- $\sqrt{3}$ D、x= $\frac{π}{3}$ 是函数f（x）的一条对称轴

查看试题解析
9. 若某几何体的三视图（单位：cm）如图所示，则此几何体的表面积等于（）

A、 $\frac{111 + 4 \sqrt{41}}{2}$ cm² B、 $\frac{111 + 3 \sqrt{41}}{2}$ cm² C、 $\frac{110 + 5 \sqrt{41}}{2}$ cm² D、 $\frac{110 + \sqrt{41}}{2}$ cm²

查看试题解析
10. 设△ABC的内角A，B，C所对边的长分别是a，b，c，且b=3，c=1，A=2B，则a的值为（）

A、 $2 \sqrt{5}$ B、4 C、 $2 \sqrt{3}$ D、 $2 \sqrt{2}$

查看试题解析
11. 已知等边△ABC的边长为2，点E，F分别在边AB、AC上，且 $\vec{A E} = λ \vec{A B}$ ， $\vec{A F} = μ \vec{A C}$ 若 $\vec{E B} \vec{· F C} = \frac{2}{3}$ ， $\vec{E C} \vec{· F B} =-1$ ，则λ+μ=（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{5}{6}$ D、 $\frac{7}{12}$

查看试题解析
12. 已知函数f（x）= $\frac{x + 1}{e^{x}}$ -ax有两个零点，则实数a的取值范围是（）

A、（0，+∞） B、（1，+∞） C、（ $\frac{2}{e}$ ，+∞） D、（0， $\frac{2}{e}$ ）

查看试题解析

二、填空题（本大题共4小题，每小题5分，共20分。）

13. 若x，y满足约束条件 ${\begin{cases} x - 2 y - 2 \leq 0 \\ x - y + 1 \geq 0 \\ y \leq 0 \end{cases}$ ，则z=4x+3y的最大值为。

查看试题解析
14. 平均数为1010的一组数构成等差数列，其末项为2019，则该数列的首项为。

查看试题解析
15. 抛物线有如下光学性质：由其焦点射出的光线经抛物线反射后，沿平行于抛物线对称轴的方向射出，现有抛物线y²=2px（p>0），如图一平行x轴的光线射向抛物线，经两次反射后沿平行x轴方向射出，若两平行光线间的最小距离为4，则该抛物线的方程为 .

查看试题解析
16. 连接正方体每个面的中心构成一个正八面体，则该八面体的外接球与内切球体积之比为。

查看试题解析

三、解答题（本大题共6小题，共70分，）

17. 已知等差数列{a_n}满足a₄=7，其前5项和为25，等比数列{b_n}的前n项和S_n=2ⁿ-1（n∈N^*）.
（I）求数列{a_n}、{b_n}的通项公式；

（Ⅱ）求数列{a_nb_n}的前n项和T_n.

查看试题解析
18. 如图，在以A，B，C，D，E，F为顶点的五面体中，面ABEF为正方形，AF= $2 \sqrt{3}$ FD，∠AFD=90°，且二面角D-AF-E与二面角C-BE-F都是30°.

（I）证明：AF⊥平面EFDC；

（Ⅱ）求直线BF与平面BCE所成角的正弦值。

查看试题解析
19. 全民健身倡导全民做到每天参加一次以上的体育健身活动，旨在全面提高国民体质和健康水平某部门在该市2013-2018年发布的全民健身指数中，对其中的“运动参与评分值y”（满分100分）进行了统计，制成如图所示的散点图。

（注：年份代码1-6分别对应年份2013-2018）

（I）根据散点图，建立y关于t的回归方程 $\hat{y} = \hat{b} t + \hat{a}$ ；

（Ⅱ）从该市的市民中随机抽取了容量为150的样本，其中经常参加体育锻炼的人数为50，以频率为概率，若从这150名市民中随机抽取4人，记其中“经常参加体育锻炼”的人数为X，求X的分布列和数学期望。

附：对于一组数据（t₁ ， y₁），（t₂ ， y₂），.…，（t_n ， y_n），其回归直线 $\hat{y} = \hat{b} t + \hat{a}$ 的斜率和截距的最小二乘估计公式分别为 $\hat{b} = \frac{\sum_{i = 1}^{n} (t_{i} - \bar{t}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(t_{i} - \bar{t})}^{2}}$ ， $\hat{a} = \hat{y} - \hat{b} t$

查看试题解析
20. 已知点A为圆B:（x+2）²+y²=32上任意一点，点C（2，0），线段AC的中垂线交AB于点M.
（I）求动点M的轨迹方程；

（Ⅱ）若动直线l与圆O:x²+y²= $\frac{8}{3}$ 相切，且与动点M的轨迹交于点E、F，求△OEF面积的最大值（O为坐标原点）.

查看试题解析
21. 已知函数f（x）=lnx+ $\frac{a}{x}$ +x（a∈R）.
（I）讨论函数f（x）的单调性；

（Ⅱ）若a=1，f（x）> $\frac{(x - k) \ln x}{x - 1}$ +x-1在（1，+∞）上恒成立，求k的取值范围.

查看试题解析
22. 在直角坐标系xOy中，曲线C₁的参数方程为 ${\begin{cases} x = 3 \cos θ \\ y = \sin θ \end{cases}$ （θ为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C₂的极坐标方程为ρ²-12ρsinθ+35=0.
（I）求曲线C₁ ， C₂的直角坐标方程；

（Ⅱ）若动直线l分别与C₁ ， C₂交于点P、Q，求|PQ|的取值范围。

查看试题解析
23. 已知函数f（x）=|2x+1|+|x-21.
（I）求不等式f（x）≥3的解集；

（Ⅱ）若不等式f（x）≤|a-1|的解集不是空集，求a的取值范围.

查看试题解析