河北省张家口市2018-2019学年高二下学期数学6月月考试卷

试卷更新日期：2019-08-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知复数 $z$ 在复平面内对应的点为 $(1,-2)$ ，（ $i$ 为虚数单位），则 $|z+1|=$ （）

A、4 B、2 C、8 D、 $2 \sqrt{2}$

查看试题解析
2. 全集 $U ={-2,-1,0,1,2}$ ，集合 $A = {x | x^{2} - x - 2 = 0}$ ， $B = {- 2, - 1}$ ， $A \cap (C_{U} B) =$ （）

A、 ${-1}$ B、 ${1}$ C、 ${2}$ D、 ${-2,-1}$

查看试题解析
3. 命题 $p : \frac{1}{x} > 1$ ，命题 $q : x > a$ ，若命题 $p$ 的必要不充分条件是 $q$ ，则 $a$ 的取值范围为（）

A、 $a < 0$ B、 $a \leq 0$ C、 $a \geq 0$ D、 $a > 0$

查看试题解析
4. 给出四个命题：①映射就是一个函数；② $f (x) = \lg (x - 3) + \sqrt{2 - x}$ 是函数；③函数 $y = f (x)$ 的图象与 $y$ 轴最多有一个交点；④ $f (x) = \sqrt{- x^{3}}$ 与 $g (x) = x \sqrt{- x}$ 表示同一个函数.其中正确的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
5. 下列说法中正确的个数是
①命题“ $\forall x \in R$ ， $x^{2} + 2 x + 2 > 0$ ”是真命题②命题“若 $x =-2$ ，则 $x^{2} + 5 x + 6 = 0$ ”的逆否命题是假命题③“ $\forall x \in R$ ， $x^{2} ⩾ 0$ ”的否定为“ $\exists x_{0} \notin R$ ， $x_{0}^{2} < 0$ ”④命题“ $\forall x \in (0, + \infty)$ ， $x > \sin x$ ”是真命题（）

A、1 B、2 C、3 D、4

查看试题解析
6. 阅读如图所示的程序框图，则输出的数据为（）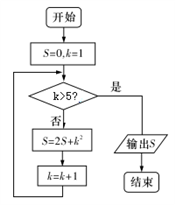

A、21 B、58 C、141 D、318

查看试题解析
7. 若函数 $f (x) = \frac{x}{\sqrt{m x^{2} - m x + 2}}$ 的定义域为 $R$ ，则实数 $m$ 取值范围是（）

A、 $[0,8)$ B、 $(8, + \infty)$ C、 $(0,8)$ D、 $(- \infty, 0) \cup (8, + \infty)$

查看试题解析

8. 调查研究某项运动与性别是否有关系得到列联表如图，若这两个变量没有关系，则

a

的可能值为（）

	男性	女性	合计
爱好运动	100	a	100+a
不爱好运动	120	600	720
合计	220	600+a	820+a

A、720 B、500 C、300 D、200

查看试题解析

9. 某大型商场共有编号为甲、乙、丙、丁、戊的五个安全出口.若同时开放其中的两个安全出口，疏散500名乘客所需的时间如下：

安全出口编号	甲，乙	乙，丙	丙，丁	丁，戊	甲，戊
疏散乘客时间（s）	120	220	160	140	200

则疏散乘客最快的一个安全出口的编号是（）

A、甲 B、乙 C、丁 D、戊

查看试题解析

10. 设 $x \in R$ ,用 $[x]$ 表示不超过 $x$ 的最大整数，已知函数 $f (x) = \frac{x^{2}}{2 x^{2} - 2 x + 1}$ ， $x \in [\frac{1}{3}, + \infty)$ ，则函数 $y =[f (x)]$ 的值域为（）

A、 ${0}$ B、 ${0,1}$ C、 ${-1,0}$ D、 ${1}$

查看试题解析
11. 点 $A (x, y)$ 是曲线 ${\begin{array}{l} x = 2 + \cos θ \\ y = 1 + 3 \sin θ \end{array}$ ，（ $θ$ 为参数）上的任意一点，则 $2 x - y$ 的最大值为（）

A、 $\sqrt{13}$ B、 $\sqrt{13} + 5$ C、3 D、 $\sqrt{13} + 3$

查看试题解析
12. 已知不等式 $2 a x^{2} + a x - 3 > 0$ 对任意的 $a \in [1, 3]$ 恒成立的 $x$ 的取值集合为 $A$ ，不等式 $m x^{2} + (m - 1) x - m > 0$ 对任意的 $x \in [1, 3]$ 恒成立的 $m$ 取值集合为 $B$ ，则有（）

A、 $A \subseteq C_{R} B$ B、 $A \subseteq B$ C、 $B \subseteq C_{R} A$ D、 $B \subseteq A$

查看试题解析

二、填空题

13. 已知集合 $A = {x | x^{2} + 2 x - 8 > 0}$ ，集合 $B = {y | y = \sqrt{x - 3}}$ ，则 $A \cap B =$ .

查看试题解析
14. 已知函数 $f (\sqrt{x} + 1) = x - 4$ ，则 $f (x)$ 的解析式为.

查看试题解析
15. 若函数 $f (x) = x^{2} + 2 x + 3$ ， $g (x) = 3^{x} + a$ ，若 $\forall x_{1} \in [- 2, 1]$ 都 $\exists x_{2} \in [1, 2]$ ，使得 $f (x_{1}) = g (x_{2})$ 成立，则实数 $a$ 的取值范围是.

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} x + 1 ， x \leq 0 \\ {(x - 1)}^{2} ， x > 0 \end{array}$ ，设函数 $g (x) = f (- x) - f (x) - a$ ，若函数 $g (x)$ 在 $R$ 上恰有两个不同的零点，则 $a$ 的值为.

查看试题解析

三、解答题

17. 已知集合 $A = {x | a < x < 2 a + 2}$ ， $B = {x | 1 < 2^{x} < 16}$ ，若 $A \cup B = B$ ，求 $a$ 的取值范围.

查看试题解析
18. 已知 $p : \frac{x^{2}}{4 - a} + \frac{y^{2}}{a + 2} = 1$ 表示椭圆， $q : x^{2} + y^{2} - 2 a y + 2 a^{2} - 9 = 0$ 表示一个圆.

(1)、若 $p$ 为真命题，求 $a$ 的取值范围；

(2)、若 $p \land q$ 为真命题，求 $a$ 的取值范围.

查看试题解析
19. 已知直线 $l$ 的参数方程为 ${\begin{array}{l} x = t \\ y = 1 \end{array}$ （ $t$ 为参数），在平面直角坐标系 $x o y$ 中，以坐标原点 $O$ 为极点， $x$ 轴的正半轴为极轴建立极坐标系，曲线 $C$ 的极坐标方程为 $ρ = 4 \sin θ$ ，若极坐标系内异于 $O$ 的三点 $A (ρ_{1} ， φ)$ ， $B (ρ_{2} ， φ + \frac{π}{3})$ ， $C (ρ_{3} ， φ - \frac{π}{3})$ 都在曲线 $C$ 上.

(1)、求证： $ρ_{1} = ρ_{2} + ρ_{3}$ ；

(2)、若 $l$ 过 $B$ ， $C$ 两点，求四边形 $O B A C$ 的面积

查看试题解析
20. 已知函数 $f (x) = {\begin{array}{l} x + 2, x ⩽ 0 \\ x^{2} + b x + c, x > 0 \end{array}$ ，若 $f (\frac{1}{2}) = f (\frac{3}{2})$ 且 $f (2) = - 3$ ，求：

(1)、函数 $f (x)$ 的解析式；

(2)、若 $g (x) =2 x - 10$ ，求函数 $y = g (f (x))$ 的零点.

查看试题解析
21. 某企业为确定下一年投入某种产品的研发费用，需了解年研发费用 $x$ （单位：千万元）对年销售量y（单位：万件）的影响，统计了近10年投入的年研发费用x，与年销售量 $y_{i} (i = 1 ， 2 ， 3 \dots 10)$ 的数据，得到散点图如图所示：

附：对于一组数据 $(u_{1} ， v_{1})$ ， $(u_{2} ， v_{2})$ …， $(u_{n} ， v_{n})$ ，其回归直线 $\bar{v} = \bar{a} + \hat{β} u$ 的斜率和截距的最小二乘估计分别为 $\hat{β} = \frac{\sum_{i = 1}^{10} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{10} (u_{i} - \bar{u})}$ ， $\hat{α} = \bar{v} - \hat{β} \bar{u}$

(1)、利用散点图判断， $y = b x + a$ 和 $y = c \cdot x^{d}$ （其中 $c ， d$ 为大于0的常数）哪一个更适合作为年研发费用 $x$ 和年销售量 $y$ 的回归方程类型（只要给出判断即可，不必说明理由）.

(2)、对数据作出如下处理：令 $u_{i} = \ln x_{i}$ ， $v_{i} = \ln y_{i}$ ，得到相关统计量的值如下表：

$\sum_{i = 1}^{10} v_{i}$

$\sum_{i = 1}^{10} u_{i}$

$\sum_{i = 1}^{10} (u_{i} - \bar{u}) (v_{i} - \bar{v})$

$\sum_{i = 1}^{10} {(u_{i} - \bar{u})}^{2}$

15

15

28.25

56.5

根据（1）的判断结果及表中数据，求 $y$ 关于 $x$ 的回归方程；

(3)、已知企业年利润z（单位：千万元）与 $x$ ， $y$ 的关系为 $z = 18 e^{- \frac{3}{4}} y - \frac{9}{2} x$ （其中 $e =2 .71828$ …），根据（2）的结果，要使得该企业下一年的年利润最大，预计下一年应投入多少研发费用?

查看试题解析
22. 在极坐标系中，曲线 $C$ 的极坐标方程为 $ρ^{2} - 2 ρ \cos θ - 3 = 0$ ，以极点为原点，极轴为 $x$ 轴的正半轴建立平面直角坐标系，直线 $l$ 的方程为 $y = k x$ .

(1)、求曲线 $C$ 的参数方程；

(2)、曲线 $C$ 与直线 $l$ 交于 $A, B$ 两点，若 $| | O A |-| O B | |=2$ ，求 $k$ 的值.

查看试题解析
23. 已知 $f (x)=| a x +2|$ .

(1)、当 $a = 2$ 时，求不等式 $f (x)>3 x$ 的解集；

(2)、若 $f (1) ⩽ M$ ， $f (2) ⩽ M$ ，证明： $M ⩾ \frac{2}{3}$ .

查看试题解析

$\sum_{i = 1}^{10} v_{i}$	$\sum_{i = 1}^{10} u_{i}$	$\sum_{i = 1}^{10} (u_{i} - \bar{u}) (v_{i} - \bar{v})$	$\sum_{i = 1}^{10} {(u_{i} - \bar{u})}^{2}$
15	15	28.25	56.5