北京市西城区2018-2019学年高一下学期数学期末考试试卷

试卷更新日期：2019-08-01 类型：期末考试

进入出卷网下载

一、单选题

1. 已知点 $P (1, 2)$ ， $Q (3, 0)$ ，则线段 $P Q$ 的中点为（）

A、 $(4, 2)$ B、 $(2, 1)$ C、 $(2, 4)$ D、 $(1, 2)$

查看试题解析
2. 直线 $l$ 经过点 $A (0, - 1)$ ， $B (1, 1)$ ，则直线 $l$ 的斜率是（）

A、 $2$ B、 $- 2$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
3. 下列直线中，与直线 $3 x + y - 2 = 0$ 平行的是（）

A、 $3 x - y = 0$ B、 $x - 3 y = 0$ C、 $3 x + y = 0$ D、 $x + 3 y = 0$

查看试题解析
4. 在空间中，给出下列四个命题：
①平行于同一个平面的两条直线互相平行；②垂直于同一个平面的两个平面互相平行；

③平行于同一条直线的两条直线互相平行；④垂直于同一个平面的两条直线互相平行．

其中正确命题的序号是（）

A、①② B、①③ C、②④ D、③④

查看试题解析
5. 圆 $x^{2} - 6 x + y^{2} - 16 = 0$ 的周长是（）

A、 $25 π$ B、 $10 π$ C、 $8 π$ D、 $5 π$

查看试题解析
6. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，若 $E ， F ， G ， H$ 分别是棱 $A_{1} B_{1} ， B B_{1} ， C C_{1} ， C_{1} D_{1}$ 的中点，则必有（）

A、 $B D_{1} ∥ G H$ B、 $B D ∥ E F$ C、平面 $E F G H ∥$ 平面 $A B C D$ D、平面 $E F G H ∥$ 平面 $A_{1} B C D_{1}$

查看试题解析
7. 一个棱长为2的正方体被一个平面截去一部分后，剩余几何体的三视图如图所示，则截去的几何体是 $($ $)$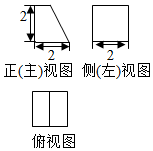

A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱

查看试题解析
8. 已知点 $A (0, 1)$ ,点 $B$ 在直线 $x + y + 1 = 0$ 上运动．当 $| A B |$ 最小时，点 $B$ 的坐标是（）

A、 $(- 1, 1)$ B、 $(- 1, 0)$ C、 $(0, - 1)$ D、 $(- 2, 1)$

查看试题解析
9. 已知圆 $O_{1}$ 的方程为 $x^{2} + y^{2} = 4$ ，圆 $O_{2}$ 的方程为 ${(x - a)}^{2} + {(y - 1)}^{2} = 1$ ，那么这两个圆的位置关系不可能是（）

A、外离 B、外切 C、内含 D、内切

查看试题解析
10. 如图，在空间四边形 $A B C D$ 中，两条对角线 $A C ， B D$ 互相垂直，且长度分别为4和6，平行于这两条对角线的平面与边 $A B ， B C ， C D ， D A$ 分别相交于点 $E ， F ， G ， H$ ，记四边形 $E F G H$ 的面积为y，设 $\frac{B E}{A B} = x$ ，则（）

A、函数 $y = f (x)$ 的值域为 $(0 ， 4]$ B、函数 $y = f (x)$ 的最大值为8 C、函数 $y = f (x)$ 在 $(0 ， \frac{2}{3})$ 上单调递减 D、函数 $y = f (x)$ 满足 $f (x) = f (1 - x)$

查看试题解析

二、填空题

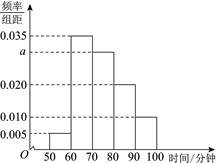
11. 直线 $y = \sqrt{3} x + 1$ 的倾斜角的大小是．

查看试题解析
12. 对于任意实数 $k$ ，直线 $y = k x + 1$ 经过的定点坐标为．

查看试题解析
13. 圆柱的高是 $2$ ，底面圆的半径是 $1$ ，则圆柱的侧面积是．

查看试题解析
14. 圆心为 $(1, 0)$ ，且与直线 $x - y = 0$ 相切的圆的方程是．

查看试题解析
15. 设三棱锥 $P - A B C$ 的三条侧棱两两垂直，且 $P A = P B = P C = 1$ ，则三棱锥 $P - A B C$ 的体积是．

查看试题解析
16. 已知点 $M (- 1, 0)$ , $N (1, 0)$ ．若直线 $l : x + y - m = 0$ 上存在点 $P$ 使得 $P M ⊥ P N$ ，则实数 $m$ 的取值范围是．

查看试题解析
17. 某公司有大量客户，且不同龄段客户对其服务的评价有较大差异．为了解客户的评价，该公司准备进行抽样调查，可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样，则最合适的抽样方法是．

查看试题解析
18. 从某校 $3000$ 名学生中随机抽取若干学生，获得了他们一天课外阅读时间（单位：分钟）的数据，整理得到频率分布直方图如下．则估计该校学生中每天阅读时间在 $[70 ， 80)$ 的学生人数为．

查看试题解析
19. 设正方形 $A B C D$ 的边长是 $2$ ，在该正方形区域内随机取一个点，则此点到点 $A$ 的距离大于 $2$ 的概率是．

查看试题解析
20. 从分别写有1,2,3,4的4张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为．

查看试题解析
21. 在△ $A B C$ 中， $a = 2$ ， $c = \sqrt{2}$ ， $\sin A + \cos A = 0$ ，则角 $B$ 的大小为．

查看试题解析

三、解答题

22. 如图，在三棱锥 $P - A B C$ 中， $P B = P C$ ， $A B = A C$ ． $D$ ， $E$ 分别是 $B C$ ， $P B$ 的中点．

（Ⅰ）求证： $D E ∥$ 平面 $P A C$ ；

（Ⅱ）求证：平面 $A B C ⊥$ 平面 $P A D$ ；

（Ⅲ）在图中作出点 $P$ 在底面 $A B C$ 的正投影，并说明理由．

查看试题解析
23. 已知圆心为 $C (4 ， 3)$ 的圆经过原点 $O$ ．
（Ⅰ）求圆 $C$ 的方程；

（Ⅱ）设直线 $3 x - 4 y + 15 = 0$ 与圆 $C$ 交于 $A$ ， $B$ 两点，求△ $A B C$ 的面积．

查看试题解析
24. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是菱形，对角线 $A C$ ， $B D$ 交于点 $O$ ．

（Ⅰ）若 $A C ⊥ P D$ ，求证： $A C ⊥$ 平面 $P B D$ ；

（Ⅱ）若平面 $P A C ⊥$ 平面 $A B C D$ ，求证： $P B = P D$ ；

（Ⅲ）在棱 $P C$ 上是否存在点 $M$ （异于点 $C$ ），使得 $B M ∥$ 平面 $P A D$ ？说明理由．

查看试题解析
25. 为缓解交通运行压力，某市公交系统实施疏堵工程．现调取某路公交车早高峰时段全程运输时间（单位：分钟）的数据，从疏堵工程完成前的数据中随机抽取5个数据，记为 $A$ 组；从疏堵工程完成后的数据中随机抽取5个数据，记为 $B$ 组．
$A$ 组： $128$ $100$ $151$ $125$ $120$

$B$ 组： $100$ $102$ $97$ $101$ $100$

（Ⅰ）该路公交车全程运输时间不超过 $100$ 分钟，称为“正点运行”．从 $A$ ， $B$ 两组数据中各随机抽取一个数据，求这两个数据对应的两次运行中至少有一次“正点运行”的概率；

（Ⅱ）试比较 $A$ ， $B$ 两组数据方差的大小（不要求计算），并说明其实际意义．

查看试题解析
26. 已知 $△ A B C$ 同时满足下列四个条件中的三个：
① $A = \frac{π}{3}$ ；② $\cos B = - \frac{2}{3}$ ；③ $a = 7$ ；④ $b = 3$ ．

（Ⅰ）请指出这三个条件，并说明理由；

（Ⅱ）求 $△ A B C$ 的面积．

查看试题解析
27. 在直角坐标系 $x O y$ 中，已知圆 $M : {(x - 3)}^{2} + {(y - 4)}^{2} = 4$ 及其上一点 $A$ ．
（Ⅰ）求 $| O A |$ 的最大值；

（Ⅱ）设 $A (3, 2)$ ，点 $T$ 在 $x$ 轴上．若圆 $M$ 上存在两点 $P$ 和 $Q$ ，使得 $\vec{T A} + \vec{T P} = \vec{T Q}$ ，求点 $T$ 的横坐标的取值范围．

查看试题解析