安徽省皖南八校2018-2019学年高二下学期文数第二次联考试卷

试卷更新日期：2019-08-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 若集合 $A = {x | x^{2} - 3 x ⩽ 0} ， B = {x | 3^{x} > 1}$ ，则 $A \cap B =$ （）

A、 $[0 ， 3]$ B、 $[1 ， 3]$ C、 $(1 ， 3]$ D、 $(0 ， 3]$

查看试题解析
2. $m \in R$ ， $i$ 为虚数单位，若 $(m + i) (2 - 3 i) = 5 - i$ ，则 $m$ 的值为（）

A、1 B、-1 C、2 D、-2

查看试题解析
3. 已知向量 $\vec{a} = (1, 5)$ ，向量 $\vec{b} = (x ， - 1)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则实数 $x$ 的值为（）

A、-5 B、5 C、-1 D、1

查看试题解析
4. 若函数 $y = {\begin{array}{l} \log_{a} x ， x ⩾ 1 \\ (4 - a) x - 1 ， x < 1 \end{array}$ ，在 $R$ 上是增函数，则实数 $a$ 的取值范围是（）

A、（1，4） B、（2，4） C、[3，4） D、（2，3]

查看试题解析
5. 如图所示是人教A版选修1-2第二章《推理与证明》的知识结构图（部分），如果要加入知识点“三段论”，那么应该放在图中（）

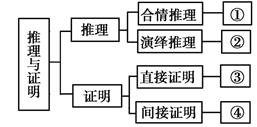A、“①”处 B、“②”处 C、“③”处 D、“④”处

查看试题解析
6. 设函数 $f (x)$ 是奇函数，定义域为 $R$ ，且满足 $f (x + 1) = - f (x)$ .当 $0 ⩽ x < 1$ 时， $f （ x ） = x - x^{2}$ ，则 $f (\frac{2020}{3}) =$ （）

A、 $- \frac{2}{9}$ B、 $- \frac{1}{4}$ C、 $\frac{2}{9}$ D、 $\frac{1}{4}$

查看试题解析
7. 下列说法正确的是（）

A、“ $x < - 1$ ”是“ $\lg (x^{2} - 9 x) > 1$ ”的必要不充分条件 B、命题“ $\exists x_{0} > 1 ， 2^{x_{0}} > 3$ ”的否定是“ $\forall x > 1 ， 2^{x} < 3$ ” C、若 $p : 1 \in {x | 2^{x} - 3^{x} < 0} ， q : 2 \in {x | \frac{1}{x - 1} > 1}$ ，则 $p \land q$ 是真命题 D、若 $\exists x_{0} \in R ， x_{0}^{2} - 2 x_{0} + m < 0$ ，则实数 $m$ 的取值范围是 $(- \infty, 1)$

查看试题解析
8. 抛线 $y^{2} = 2 p x (p > 0)$ 的焦点为 $F$ ，准线为 $l$ ， $l$ 与 $x$ 轴的交点为 $A$ ，点 $B$ 在 $l$ 上，直线 $F B$ 的倾斜角为 $45 °$ ，且 $\vec{F A} \cdot \vec{F B} = 4$ ，则 $△ A B F$ 的面积为（）

A、 $\sqrt{2}$ B、 $2$ C、 $2 \sqrt{2}$ D、 $4$

查看试题解析
9. 执行如围所示的程序框围，若输出的 $S$ 的值为 $\frac{7}{2}$ ，则实数 $k$ 的取值范围为（）

A、 $[64 ， 128)$ B、 $[32 ， 64)$ C、 $[16 ， 48)$ D、 $(32 ， 64)$

查看试题解析

10. 将正整数依次排列如下：

1
2	3
4	5	6
7	8	9	10
11	12	13	14	15
16	17	18	19	20	21
…	…	…	…	…	…

由表知第5行第3列的数是13，若第2020行第2列的数是 $a$ ，则 $a$ 的各位数字中，数字0的个数为（）

A、0 B、1 C、2 D、3

查看试题解析

11. 已知函数 $f (x) = \sin (ω x + \frac{π}{6}) + \frac{1}{2} (ω > 0 ， x \in R)$ ，且 $f (α) = - \frac{1}{2} ， f (β) = \frac{1}{2}$ ，若 $| α - β |$ 的最小值为 $\frac{π}{4}$ ，则 $f (x)$ 的图象（）

A、关于点 $(π ， \frac{1}{2})$ 对称 B、关于点 $(\frac{5 π}{12} ， \frac{1}{2})$ 对称 C、关于直线 $x = - \frac{π}{12}$ 对称 D、关于直线 $x = π$ 对称

查看试题解析

12. 某次测试中有4道选择题，每题1分，每道题在选项

A 、 B 、 C

中只有一个是正确的.下表是甲、乙、丙三名同学每道题填涂的答案和这4道题的得分：

	1	2	3	4	得分
甲	C	A	B	A	3
乙	C	C	B	C	2
丙	B	B	B	A	1

则甲同学答错的题目的题号是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 设复数 $z_{1} = 2 + i ， z_{2} = m + 2 i$ （ $m \in R ， i$ 为虚数单位），若 $z_{1} z_{2}$ 为纯虚数，则 $m$ 的值为.

查看试题解析
14. 化简 $\log_{2.5} 6.25 + \lg 0.001 + 2 \ln \sqrt{e} - 2^{1 + \log_{2} 3} =$ .

查看试题解析
15. 某公司咨询顾客对一件新产品的满意度.甲说：“丙满意.”乙说：“我不满意.”丙说：“丁满意.”丁说：“我不满意.”已知他们之间相互了解情况四人中只有一人说了真话，只有一人满意此产品.根据以上条件，可以判定满意此产品的人是.

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} 2^{x} ， x > 1 \\ 3 - x ， x ⩽ 1 \end{array}$ .若函数 $y = f (x) - k x - 4$ 有两个零点，则实数 $k$ 的取值范围是.

查看试题解析

三、解答题

17. 在 $△ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，已知 $(a + b) (a - b) = c (c - b)$ .

(1)、求角 $A$ 的大小；

(2)、若 $a = b \cos C ， c = 2$ ，求 $△ A B C$ 的面积.

查看试题解析

18. 为了解某班学生喜爱打篮球是否与性别有关，对本班45人进行了问卷调查得到了如下的列联表：

	喜爱打篮球	不喜爱打篮球	合计
男生		5
女生	5
合计			45

已知在全部45人中随机抽取1人，是男同学的概率为 $\frac{5}{9}$

附参考公式： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)} ， n = a + b + c + d$

$P (K^{2} ⩾ k_{0})$	0.15	0，10	0.05	0.025	0.010	0.005	0.001
$k_{0}$	2.072	2.706	3.841	5.024	6.635	7.879	10.828

(1)、请将上面的列联表补充完整；

(2)、是否有

99.9 %

的把握认为喜爱打篮球与性别有关，请说明理由。

查看试题解析

19. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，已知 $E ， F$ 分别是 $A_{1} C_{1} ， B C$ 的中点

(1)、求证： $C_{1} F ∥$ 平面 $A B E$ ；

(2)、若 $A A_{1} ⊥$ 平面 $A B C ， A B ⊥ B C ， A A_{1} = A B = B C = 2$ ，求三棱锥 $C_{1} - A B E$ 的体积.

查看试题解析

20. 某小组为了研究昼夜温差对一种稻谷种子发芽情况的影响，他们分别记录了4月1日至4月5日的每天星夜温差与实验室每天每100颗种子的发芽数，得到如下资料：

日期	4月1日	4月2日	4月3日	4月4日	4月5日
温差 $x (° C)$	9	10	11	8	12
发芽数 $y$ （颗）	38	30	24	41	17

利用散点图，可知 $x ， y$ 线性相关。

（公式： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}} ， \hat{a} = \bar{y} - b \bar{x}$ ）

(1)、求出

y

关于

x

的线性回归方程，若4月6日星夜温差

5 ° C

，请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数；

(2)、若从4月1日

\sim

4月5日的五组实验数据中选取2组数据，求这两组恰好是不相邻两天数据的概率.

查看试题解析

21. 已知椭圆 $C$ 的焦点在坐标轴上，对称中心为坐标原点，且过点 $M (1 ， \frac{\sqrt{6}}{2})$ 和 $N (\sqrt{2} ， 1)$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、设直线 $l$ 交椭圆 $C$ 于 $A ， B$ 两点，坐标原点 $O$ 到直线 $l$ 的距离为 $\frac{2 \sqrt{3}}{3}$ ，求证： $∠ A O B$ 是定值.

查看试题解析
22. 已知函数f（x）＝xe^x﹣ax²﹣x；

(1)、若f（x）在x＝﹣1处取得极值，求a的值及f（x）的单调区间；

(2)、当x＞1时，f（x）＞0恒成立，求a的取值范围．

查看试题解析