辽宁省丹东市凤城市2018-2019学年高二下学期数学5月月考试卷
试卷更新日期:2019-07-30 类型:月考试卷
一、单选题
-
1. 设集合 ,则 ( )
A、 B、 C、 D、2. 已知复数 满足 ,则 ( )A、 B、 C、 D、3. 已知向量 , 满足 , ,则 ( )A、4 B、3 C、2 D、04. 函数 的部分图象如图所示,则( ) A、 B、 C、 D、5. 函数 的图像大致为 ( )A、
A、 B、 C、 D、5. 函数 的图像大致为 ( )A、 B、
B、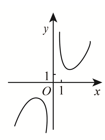 C、
C、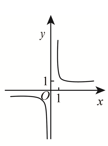 D、
D、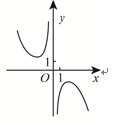 6. 圆 的圆心到直线 的距离为1,则 ( )A、 B、 C、 D、27. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
6. 圆 的圆心到直线 的距离为1,则 ( )A、 B、 C、 D、27. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( ) A、 B、 C、 D、8. 若 ,则双曲线 的离心率的取值范围是( )A、 B、 C、 D、9. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩。老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩。看后甲对大家说:我还是不知道我的成绩。根据以上信息,则( )A、乙可以知道四人的成绩 B、丁可以知道四人的成绩 C、乙、丁可以知道对方的成绩 D、乙、丁可以知道自己的成绩10. 已知函数f(x)= ,下列结论中错误的是( )A、 , f( )=0 B、函数y=f(x)的图像是中心对称图形 C、若 是f(x)的极小值点,则f(x)在区间(-∞, )单调递减 D、若 是f(x)的极值点,则 ( )=011. 过抛物线C:y2=4x的焦点F,且斜率为 的直线交C于点M(M在x轴上方),l为C的准线,点N在l上,且MN⊥l,则M到直线NF的距离为( )A、 B、2 C、2 D、312. 若存在正数x使2x(x-a)<1成立,则a 的取值范围是( )A、(-∞,+∞) B、(-2, +∞) C、(0, +∞) D、(-1,+∞)
A、 B、 C、 D、8. 若 ,则双曲线 的离心率的取值范围是( )A、 B、 C、 D、9. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩。老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩。看后甲对大家说:我还是不知道我的成绩。根据以上信息,则( )A、乙可以知道四人的成绩 B、丁可以知道四人的成绩 C、乙、丁可以知道对方的成绩 D、乙、丁可以知道自己的成绩10. 已知函数f(x)= ,下列结论中错误的是( )A、 , f( )=0 B、函数y=f(x)的图像是中心对称图形 C、若 是f(x)的极小值点,则f(x)在区间(-∞, )单调递减 D、若 是f(x)的极值点,则 ( )=011. 过抛物线C:y2=4x的焦点F,且斜率为 的直线交C于点M(M在x轴上方),l为C的准线,点N在l上,且MN⊥l,则M到直线NF的距离为( )A、 B、2 C、2 D、312. 若存在正数x使2x(x-a)<1成立,则a 的取值范围是( )A、(-∞,+∞) B、(-2, +∞) C、(0, +∞) D、(-1,+∞)二、填空题
-
13. 曲线 在点 处的切线方程为 .14. 长方体的长,宽,高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为.15. 的内角 的对边分别为 ,若 ,则 .16. 已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a= .
三、解答题
-
17. 已知 是递增的等差数列, , 是方程 的根
(Ⅰ)求 的通项公式;
(Ⅱ)求数列 的前 项和.
18. 如图,四棱锥 中,底面 为矩形, 平面 , 为 的中点.
(Ⅰ)证明: 平面 ;
(Ⅱ)设 , ,三棱锥 的体积 ,求 到平面 的距离.
19. 海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:
 (1)、记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;(2)、填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
(1)、记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;(2)、填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:箱产量<50kg
箱产量≥50kg
旧养殖法
新养殖法
(3)、根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较。附:
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
20. 在直角坐标系 中,点P到两点 的距离之和等于4,设点P的轨迹为C.(1)、求曲线C的方程;(2)、过点 作直线l与曲线C交于点A、B,以线段 为直径的圆能否过坐标原点,若能,求出直线l的方程,若不能请说明理由.