2017年浙江省衢州市中考数学试卷
试卷更新日期:2017-06-14 类型:中考真卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. -2的倒数是( )A、 B、 C、-2 D、22.
下图是由四个相同的小立方块搭成的几何体,它的主视图是( )
 A、
A、 B、
B、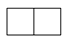 C、
C、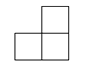 D、
D、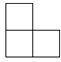 3. 下列计算正确的是( )A、 B、 C、 D、4. 据调查,某班20位女同学所穿鞋子的尺码如下表所示,则鞋子尺码的众数和中位数分别是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 据调查,某班20位女同学所穿鞋子的尺码如下表所示,则鞋子尺码的众数和中位数分别是( )尺码(码)
34
35
36
37
38
人数
2
5
10
2
1
A、 35码,35码 B、35码,36码 C、36码,35码 D、36码,36码5.如图,AB∥CD,∠A=70°,∠C=40°,则∠E等于( )
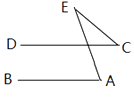 A、 30° B、40° C、60° D、70°6. 二元一次方程组 的解是( )A、 B、 C、 D、7.
A、 30° B、40° C、60° D、70°6. 二元一次方程组 的解是( )A、 B、 C、 D、7.下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线。则对应作法错误的是( )
 A、 ① B、② C、③ D、④8.
A、 ① B、② C、③ D、④8.如图,在直角坐标系中,点A在函数 的图象上,AB⊥ 轴于点B,AB的垂直平分线与 轴交于点C,与函数 的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )
 A、 2 B、 C、4 D、9.
A、 2 B、 C、4 D、9.如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
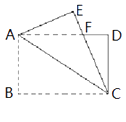 A、 B、 C、 D、10.
A、 B、 C、 D、10.运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。则图中阴影部分的面积是( )
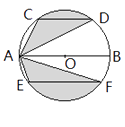 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 二次根式 中字母 的取值范围是12. 计算:13. 在一个箱子里放有1个白球和2个红球,它们除颜色外其余都相同。从箱子里摸出1个球,则摸到红球的概率是14.
如图,从边长为 的正方形纸片中剪去一个边长为3的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠,无缝隙),则拼成的长方形的另一边长是
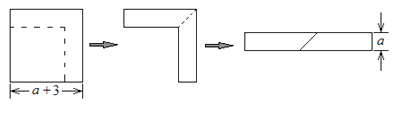 15.
15.如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线 上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是
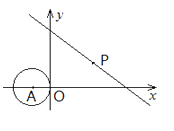 16.
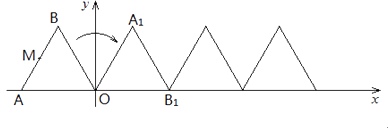
16.如图,正△ABO的边长为2,O为坐标原点,A在 轴上,B在第二象限。△ABO沿 轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是;翻滚2017次后AB中点M经过的路径长为.
三、解答题(本题有8小题,共66分)
-
17. 计算:18.
解下列一元一次不等式组:
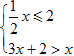 19.
19.如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9
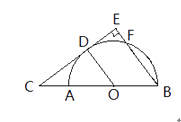 (1)、求证:△COD∽△CBE;(2)、求半圆O的半径 的长20.
(1)、求证:△COD∽△CBE;(2)、求半圆O的半径 的长20.根据衢州市统计局发布的统计数据显示,衢州市近5年国民生产总值数据如图1所示,2016年国民生产总值中第一产业、第二产业、第三产业所占比例如图2所示。
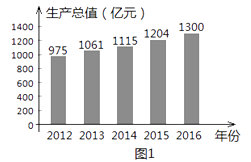
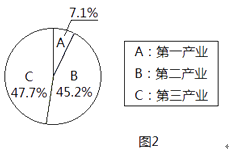
请根据图中信息,解答下列问题:
(1)、求2016年第一产业生产总值(精确到1亿元);(2)、2016年比2015年的国民生产总值增加了百分之几(精确到1%)?(3)、若要使2018年的国民生产总值达到1573亿元,求2016年至2018年我市国民生产总值平均年增长率(精确到1%)。21.“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
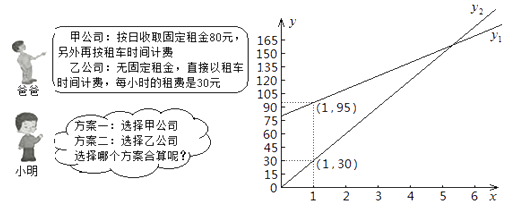
根据以上信息,解答下列问题:
(1)、设租车时间为 小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为 元,分别求出 , 关于 的函数表达式;(2)、请你帮助小明计算并选择哪个出游方案合算。22.定义:如图1,抛物线 与 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 ,则称点P为抛物线 的勾股点。
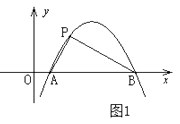
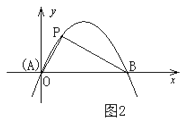 (1)、直接写出抛物线 的勾股点的坐标;(2)、如图2,已知抛物线C: 与 轴交于A,B两点,点P(1, )是抛物线C的勾股点,求抛物线C的函数表达式;(3)、在(2)的条件下,点Q在抛物线C上,求满足条件 的点Q(异于点P)的坐标23.
(1)、直接写出抛物线 的勾股点的坐标;(2)、如图2,已知抛物线C: 与 轴交于A,B两点,点P(1, )是抛物线C的勾股点,求抛物线C的函数表达式;(3)、在(2)的条件下,点Q在抛物线C上,求满足条件 的点Q(异于点P)的坐标23.问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
 (1)、△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;(2)、△DEF是否为正三角形?请说明理由;(3)、进一步探究发现,△ABD的三边存在一定的等量关系,设 , , ,请探索 , , 满足的等量关系。24.
(1)、△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;(2)、△DEF是否为正三角形?请说明理由;(3)、进一步探究发现,△ABD的三边存在一定的等量关系,设 , , ,请探索 , , 满足的等量关系。24.在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连结OB,D为OB的中点。点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF。已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。
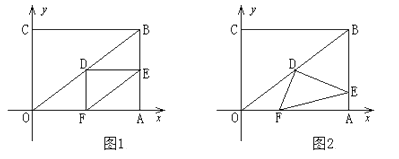 (1)、如图1,当t=3时,求DF的长;(2)、如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;(3)、连结AD,当AD将△DEF分成的两部分面积之比为1:2时,求相应t的值。
(1)、如图1,当t=3时,求DF的长;(2)、如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;(3)、连结AD,当AD将△DEF分成的两部分面积之比为1:2时,求相应t的值。