浙江省宁波十校2019届高三数学5月适应性考试试卷
试卷更新日期:2019-07-29 类型:高考模拟
一、选择题:本大题共10小题,每小题4分,共40分
-
1. 已知集合M={x∈Zlx2-x-6≤0},N={xl1≤x≤3},则M∩N=( )A、[1,3) B、[1,3] C、{1,2} D、{1,2,3}2. 双曲线5y2-4x2=20的渐近线方程是( )A、y=± x B、y=± x C、y=± x D、y=± x3. 从装有1个黑球,2个白球和2个红球的盒子里随机拿出2个小球,记拿到红球的个数为ξ,则E(ξ)为( )A、 B、 C、 D、4. 已知△ABC的三个内角分别是A.B,C,p:cosC> ,g:C∈( 0, ),则p是q的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 函数f(x)=(x- )sin2x(-π≤x≤π且x≠0)的图象可能的是( )A、
 B、
B、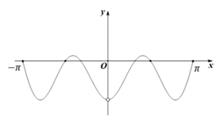 C、
C、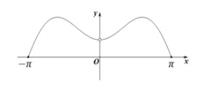 D、
D、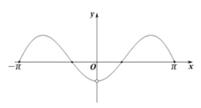 6. 在(x-2)2019的二项展开式中,含x的奇次幂的项之和为M,含x的偶次幂的项之和为N,则当x=-1时,M-N=( )A、(-3)2019 B、-1 C、1 D、320197. 一个几何体的三视图如图所示(单位:cm),则该几何体的正视图侧视图体积是( )cm3 .
6. 在(x-2)2019的二项展开式中,含x的奇次幂的项之和为M,含x的偶次幂的项之和为N,则当x=-1时,M-N=( )A、(-3)2019 B、-1 C、1 D、320197. 一个几何体的三视图如图所示(单位:cm),则该几何体的正视图侧视图体积是( )cm3 .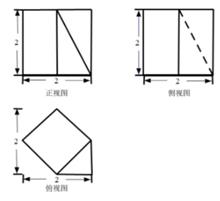 A、 B、 C、 D、8. 已知数列{an}的通项公式an=ln(1+( )n),其前n项和为Sn , 且Sn<m对任意正整数n均成立,则正整数m的最小值为( )A、2 B、4 C、6 D、89. 已知函数f(x)= ,的最小值是a2+a,则实数a的取值范围是( )A、 B、 或a= C、 D、 或a=10. 如图,点P是平面ABC外一点,点D是边AC上的动点(不含端点),且满足PD=PA,PB=BA=BC=2,∠ABC= ,则四面体P-BCD体积的最大值是( )
A、 B、 C、 D、8. 已知数列{an}的通项公式an=ln(1+( )n),其前n项和为Sn , 且Sn<m对任意正整数n均成立,则正整数m的最小值为( )A、2 B、4 C、6 D、89. 已知函数f(x)= ,的最小值是a2+a,则实数a的取值范围是( )A、 B、 或a= C、 D、 或a=10. 如图,点P是平面ABC外一点,点D是边AC上的动点(不含端点),且满足PD=PA,PB=BA=BC=2,∠ABC= ,则四面体P-BCD体积的最大值是( )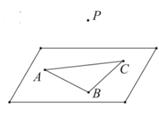 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
-
11. 加斯帕尔·蒙日是19世纪著名的几何学家,创立了画法几何学,推动了空间解析几何学的独立发展。他给出了蒙日圆的定义,即:“在椭圆中,任意两条互相垂直的切线的交点都在同一个圆上,它的圆心是椭圆中心,半径等于长半轴与短半轴平方和的算术平方根”.已知椭圆方程为: =1,写出该椭圆任意两条互相垂直的切线的交点形成的圆的方程 , 过点(3,6)且与该圆相切的直线的一般方程为 .12. 已知复数z= ,则|z|= , z2019= .13. 若实数x,y满足约束条件 ,则z= x-y最小值是 , x2+y2的最小值是 .14. 已知△ABC中,角A,B,C所对的边分别为a,b,c,△ABC的面积S=2a2sinC.
(Ⅰ) = ,
(Ⅱ)若c=10,角C的平分线CM交边AB于点M,且|CM|=4,则b= .
15. 五一假期从5月1日至4日调休4天,某班6名同学准备五一期间去参加社会实践做志愿者,每人社会实践一天,且甲乙两人不在同一天的不同安排方案有种(用数字作答).16. 如图,过抛物线焦点F的直线交抛物线C1:y2=4x于A,B两点,且|AF|=4,双曲线C2: =1(a>0,b>0)过点.B,则双曲线的离心率是 .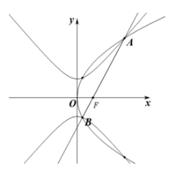 17. 已知向量a,b,c满足|a|= |b|=|c|=1,a-b=1,则 的取值范围是 .
17. 已知向量a,b,c满足|a|= |b|=|c|=1,a-b=1,则 的取值范围是 .三、解答题:本大题共5小题,共74分;
-
18. 已知偶函数f(x)=Asin(ωx+ )(A>0,ω>0,0< <π)的最大值为3,其图象与直线y=-3的某两个交点的横坐标为x1 , x2 , 且|x1-x2|的最小值为π.
(Ⅰ)求函数f(x)的解析式,并写出f(x)单调递减区间;
(Ⅱ)设函数s(x)=f(x- ),求g(x)在区间[ , ]上的值域。
19. 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是菱形,∠ABC= ,∠B1BA=∠B1BC,∠B1BD= ,AB=2A1B1=2,B1B=2,E是CD的中点.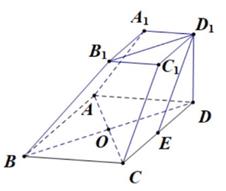
(Ⅰ)求证:直线AC⊥平面BDD1B1;
(Ⅱ)求直线ED1与平面ABB1A1所成角的正弦值。
20. 已知数列{an}的前n项和为Sn , 且Sn=n2 , n∈N*,数列{bn}满足:b1=1,b2= ,且3bn+2-4bn+1+bn=0,n∈N*.(Ⅰ)求证:数列{bn+1 , -bn}是等比数列;
(Ⅱ)求数列{an}与{bn}的通项公式;
(Ⅲ)设cn= ,数列{cn}的前n项和为了Tn , 求证:Tn<
