2017年浙江省金华市中考数学试卷

试卷更新日期：2017-06-13 类型：中考真卷

进入出卷网下载

一、选择题(本题有10小题,每小题3分,共30分)

1. 下列各组数中，把两数相乘，积为1的是（）

A、2和-2 B、-2和 $\frac{1}{2}$ C、 $\sqrt{3}$ 和 $\frac{\sqrt{3}}{3}$ D、 $\sqrt{3}$ 和- $\sqrt{3}$

查看试题解析
2.
一个几何体的三视图如图所示，这个几何体是（ )

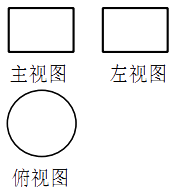A、球 B、圆柱 C、圆锥 D、立方体

查看试题解析
3. 下列各组数中，不可能成为一个三角形三边长的是（ )

A、2，3，4 B、5，7，7 C、5，6，12 D、6，8，10

查看试题解析
4. 在直角三角形Rt $Δ$ ABC中， $∠$ C=90°，AB=5，BC=3，则tanA的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
5. 在下列的计算中，正确的是（ )

A、m³+m²=m⁵ B、m⁵÷m²=m³ C、(2m)³=6m³ D、(m+1)² =m²+1

查看试题解析
6. 对于二次函数y=−(x−1)²+2的图象与性质，下列说法正确的是（ )

A、对称轴是直线x=1，最小值是2 B、对称轴是直线x=1，最大值是2 C、对称轴是直线x=−1，最小值是2 D、对称轴是直线x=−1，最大值是2

查看试题解析
7.
如图，在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片，则弓形弦AB的长为（ )

A、10cm B、16cm C、24cm D、26cm

查看试题解析
8. 某校举行以“激情五月，唱响青春”为主题的演讲比赛．决赛阶段只剩下甲、乙、丙、丁四名同学，则甲、乙同学获得前两名的概率是（ )

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
9. 若关于x的一元一次不等式组 ${\begin{matrix} 2 x- 1 > 3 （ x- 2 ）， \\ x < m \end{matrix}$ 的解是x<5,则m的取值范围是（ )

A、m≥5 B、m>5 C、m≤5 D、m<5

查看试题解析
10.
如图，为了监控一不规则多边形艺术走廊内的活动情况，现已在A，B两处各安装了一个监控探头（走廊内所用探头的观测区域为圆心角最大可取到180°的扇形），图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到，还需再安装一个监控探头，则安装的位置是（ )

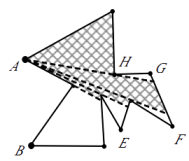A、E处 B、F处 C、G处 D、H处

查看试题解析

二、填空题 (本题有6小题,每小题4分,共24分)

11. 分解因式： $x^{2} - 4 =$

查看试题解析
12. 若 $\frac{a}{b} = \frac{2}{3} ，则 \frac{a+b}{b} =$

查看试题解析
13. 2017年5月28日全国部分宜居城市最高气温的数据如下：
宜居城市
大连
青岛
威海
金华
昆明
三亚
最高气温（℃）
25
28
35
30
26
32
则以上最高气温的中位数为℃.

查看试题解析
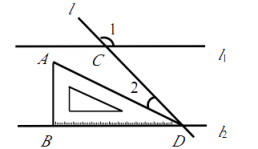
14.
如图，已知l₁//l₂ ，直线l与l₁ ， l₂相交于C，D两点，把一块含30°角的三角尺按如图位置摆放．若∠1=130°，则∠2=°.

查看试题解析
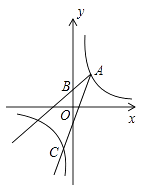
15.
如图，已知点A(2，3)和点B(0，2)，点A在反比例函数y= $\frac{k}{x}$ 的图象上.作射线AB，再将射线AB绕点A按逆时针方向旋转45°，交反比例函数图象于点C，则点C的坐标为.

查看试题解析
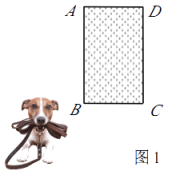
16.
在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S（m²）.
①如图1，若BC＝4m，则S＝m.
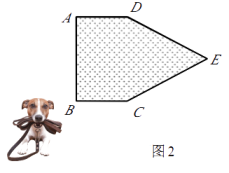
②如图2，现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其它条件不变.则在BC的变化过程中，当S取得最小值时，边BC的长为m.

查看试题解析

三、解答题（本题有8小题，共66分，各小题都必须写出解答过程）

17. 计算：2cos60°+(−1)²⁰¹⁷+|−3|−(2−1)⁰.

查看试题解析
18. 解分式方程： $\frac{2}{x+ 1} = \frac{1}{x- 1}$ .

查看试题解析
19.
如图，在平面直角坐标系中，△ABC各顶点的坐标分别为A(−2，−2)，B(−4，−1），C(−4，−4)．

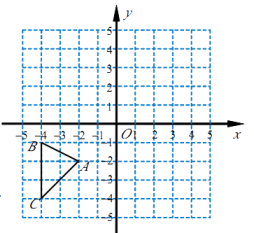(1)、作出 $Δ$ ABC关于原点O成中心对称的 $Δ$ A₁B₁C₁.

(2)、作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 $Δ$ A₁B₁C₁的内部（不包括顶点和边界），求a的取值范围.

查看试题解析
20.
某校为了解学生体质情况，从各年级学生中随机抽取部分学生进行体能测试.
每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制成图表时发现，优秀漏统计4人，良好漏统计6人，于是及时更正，从而形成如下图表.请按正确数据解答下列各题：

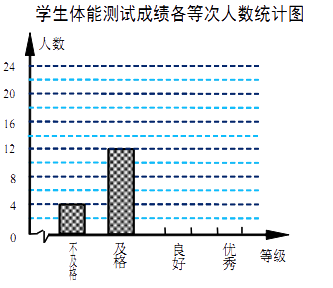(1)、填写统计表.

(2)、根据调整后数据，补全条形统计图.

(3)、若该校共有学生1500人，请你估算出该校体能测试等级为“优秀”的人数．

查看试题解析
21.
甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分. 如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 $y=a （ x-4 ）^{2} +h$ ，已知点O与球网的水平距离为5m，球网的高度1.55m.

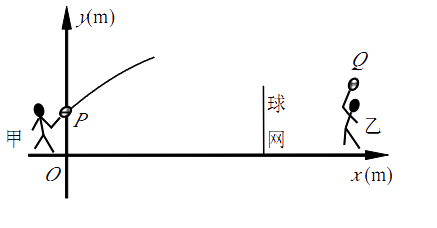(1)、当a=− $\frac{1}{24}$ 时，①求h的值.②通过计算判断此球能否过网.

(2)、若甲发球过网后，羽毛球飞行到与点O的水平距离为7m，离地面的高度为 $\frac{12}{5}$ m的Q处时，乙扣球成功，求a的值.

查看试题解析
22.
如图，已知：AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D.E是AB延长线上一点，CE交⊙O于点F，连结OC，AC.

(1)、求证：AC平分∠DAO.

(2)、若∠DAO=105°，∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 $\sqrt{2}$ ，求线段EF的长.

查看试题解析
23.
如图1，将△ABC纸片沿中位线EH折叠，使点A的对称点D落在BC边上，再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF，HG折叠，折叠后的三个三角形拼合形成一个矩形.类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形.

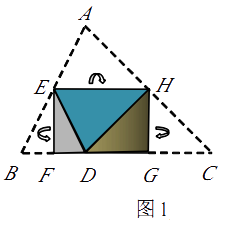
(1)、将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG，则操作形成的折痕分别是线段，；S矩形AEFG：S□ABCD=

(2)、ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH，若EF=5，EH=12，求AD的长.

(3)、如图4，四边形ABCD纸片满足AD∥BC，AD<BC，AB⊥BC，AB=8，CD=10.小明把该纸片折叠，得到叠合正方形.请你帮助画出叠合正方形的示意图，并求出AD，BC的长.

查看试题解析
24.
如图1，在平面直角坐标系中，四边形OABC各顶点的坐标分别O(0，0)，A(3，3 $\sqrt{3}$ )，B(9，5 $\sqrt{3}$ )，C(14，0).动点P与Q同时从O点出发，运动时间为t秒，点P沿OC方向以1单位长度/秒的速度向点C运动，点Q沿折线OA−AB−BC运动，在OA，AB，BC上运动的速度分别为3， $\sqrt{3}$ ， $\frac{5}{2}$ (单位长度/秒)﹒当P，Q中的一点到达C点时，两点同时停止运动．

(1)、求AB所在直线的函数表达式.

(2)、如图2，当点Q在AB上运动时，求△CPQ的面积S关于t的函数表达式及S的最大值.

(3)、在P，Q的运动过程中，若线段PQ的垂直平分线经过四边形OABC的顶点，求相应的t值.

查看试题解析

宜居城市	大连	青岛	威海	金华	昆明	三亚
最高气温（℃）	25	28	35	30	26	32