广西南宁市“4N”高中联合体2018-2019学年高一下学期期末数学试题
试卷更新日期:2019-07-25 类型:期末考试
一、单选题
-
1. 已知集合 , ,则 =( )A、 B、 C、 D、2. 现要完成下列3项抽样调查:
①从15种疫苗中抽取5种检测是否合格.②某中学共有480名教职工,其中一线教师360名,行政人员48名,后勤人员72名.为了解教职工对学校校务公开方面的意见,拟抽取一个容量为20的样本.③某中学报告厅有28排,每排有35个座位,一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请28名听众进行座谈.较为合理的抽样方法是( )
A、①简单随机抽样, ②分层抽样, ③系统抽样 B、①简单随机抽样, ②系统抽样, ③分层抽样 C、①系统抽样,②简单随机抽样, ③分层抽样 D、①分层抽样,②系统抽样, ③简单随机抽样3. 若角 的终边经过点 ,则( )A、 B、 C、 D、4. 过点 且与直线 垂直的直线方程是( )A、 B、 C、 D、5. 若 ,则 的终边在( )A、第一或第二象限 B、第一或第三象限 C、第一或第四象限 D、第二或第四象限6. 某几何体的三视图如图所示,则其体积为( )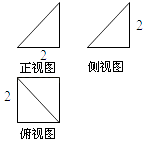 A、4 B、 C、 D、7. 执行如图所示的程序框图,则输出的值为( )
A、4 B、 C、 D、7. 执行如图所示的程序框图,则输出的值为( )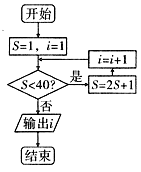 A、4 B、5 C、6 D、78. 已知函数 ,将函数 的图象向右平移 后得到函数 的图象,则下列描述正确的是( )A、 是函数 的一个对称中心 B、 是函数 的一条对称轴 C、 是函数 的一个对称中心 D、 是函数 的一条对称轴9. 圆心为点 ,并且截直线 所得的弦长为 的圆的方程( )A、 B、 C、 D、10. 函数 的部分图象如图所示,则 的值为( )
A、4 B、5 C、6 D、78. 已知函数 ,将函数 的图象向右平移 后得到函数 的图象,则下列描述正确的是( )A、 是函数 的一个对称中心 B、 是函数 的一条对称轴 C、 是函数 的一个对称中心 D、 是函数 的一条对称轴9. 圆心为点 ,并且截直线 所得的弦长为 的圆的方程( )A、 B、 C、 D、10. 函数 的部分图象如图所示,则 的值为( )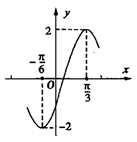 A、 B、 C、 D、11. 明清时期,古镇河口因水运而繁华.若有一商家从石塘沿水路顺水航行,前往河口,途中因故障停留一段时间,到达河口后逆水航行返回石塘,假设货船在静水中的速度不变,水流速度不变,若该船从石塘出发后所用的时间为x(小时)、货船距石塘的距离为y(千米),则下列各图中,能反映y与x之间函数关系的大致图象是( )A、
A、 B、 C、 D、11. 明清时期,古镇河口因水运而繁华.若有一商家从石塘沿水路顺水航行,前往河口,途中因故障停留一段时间,到达河口后逆水航行返回石塘,假设货船在静水中的速度不变,水流速度不变,若该船从石塘出发后所用的时间为x(小时)、货船距石塘的距离为y(千米),则下列各图中,能反映y与x之间函数关系的大致图象是( )A、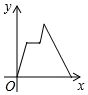 B、
B、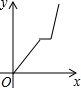 C、
C、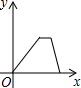 D、
D、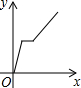 12. 在直角三角形 中, , ,点 在 斜边 的中线 上,则 的最大值为( )A、 B、 C、 D、
12. 在直角三角形 中, , ,点 在 斜边 的中线 上,则 的最大值为( )A、 B、 C、 D、二、填空题
-
13. 已知直线 的方程为 ,则直线 的倾斜角为14. 向量a,b的夹角为120°,且 ,则 等于15. 在区间 上随机取一个数x , 则 的值在 之间的概率为;16. 侧棱长为 的正三棱锥 的侧面都是直角三角形,且四个顶点都在一个球面上,则该球的表面积为 .
三、解答题
-
17. 已知 ,且 为第二象限角.
(Ⅰ)求 的值;
(Ⅱ)求 的值.
18. 已知向量(1)、若 ,求 ;(2)、若 ,求向量 在 方向上的投影.19. 如图所示,在三棱柱 中, 与 都为正三角形,且 平面 , 分别是 的中点.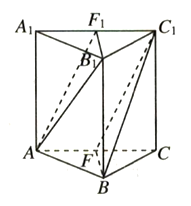
求证:
(1)、平面 平面 ;(2)、平面 平面 .20. 下表是某地一家超市在2018年一月份某一周内周2到周6的时间 与每天获得的利润 (单位:万元)的有关数据.星期
星期2
星期3
星期4
星期5
星期6
利润
2
3
5
6
9
参考公式:
(1)、根据上表提供的数据,用最小二乘法求线性回归直线方程 ;(2)、估计星期日获得的利润为多少万元.21. 已知向量 , ,函数(1)、求函数 的单调增区间(2)、将函数 的图象向左平移 个单位,得到函数 的图象,求 在 上的值域.22. 树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占 .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组 ,第2组 ,第3组 ,第4组 ,第5组 ,得到的频率分布直方图如图所示.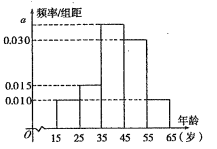 (1)、求出 的值;(2)、现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
(1)、求出 的值;(2)、现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.