广东省深圳市盐田区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-24 类型:期末考试
一、选择题:本题共12小题,每小题3分,共36分.
-
1. ( )A、4 B、1 C、 D、-42. 如图,把河AB中的水引到C,拟修水渠中最短的是( )
 A、CM B、CN C、CP D、CQ3. (-a2·b)3=( )A、-a6b3 B、a6b3 C、-a8b3 D、a8b34. 下列图形中,对称轴条数最多的是( )A、线段 B、角 C、等边三角形 D、正方形5. 如图,AB⊥BC,OB=OC,CD⊥BC,点A,O,D在一条直线上,通过测量CD的长可知小河的宽AB.由此判定△AOB≌△DOC的依据是( )
A、CM B、CN C、CP D、CQ3. (-a2·b)3=( )A、-a6b3 B、a6b3 C、-a8b3 D、a8b34. 下列图形中,对称轴条数最多的是( )A、线段 B、角 C、等边三角形 D、正方形5. 如图,AB⊥BC,OB=OC,CD⊥BC,点A,O,D在一条直线上,通过测量CD的长可知小河的宽AB.由此判定△AOB≌△DOC的依据是( )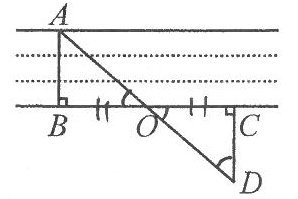 A、SAS或SSA B、ASA或AAS C、SAS或ASA D、SSS或AAS6. 在一列火车匀速通过隧道(已知隧道长度大于火车长度)的过程中,火车在隧道内的部分的长度s与火车通过隧道的时间(从车头进到车尾出止)t之间的关系是( )A、
A、SAS或SSA B、ASA或AAS C、SAS或ASA D、SSS或AAS6. 在一列火车匀速通过隧道(已知隧道长度大于火车长度)的过程中,火车在隧道内的部分的长度s与火车通过隧道的时间(从车头进到车尾出止)t之间的关系是( )A、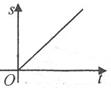 B、
B、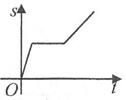 C、
C、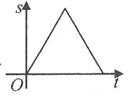 D、
D、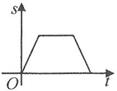 7. 将一张长方形纸片按下列顺序对折两次,然后在对折后的纸片上剪出一个太阳形小洞.将纸片展开,得到的图形是( )
7. 将一张长方形纸片按下列顺序对折两次,然后在对折后的纸片上剪出一个太阳形小洞.将纸片展开,得到的图形是( ) A、
A、 B、
B、 C、
C、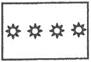 D、
D、 8. 下列事件中,是确定事件的是( )A、古筝弹得好歌就唱得好 B、昨天太阳从西边升起 C、网红看过电影《少年的你》 D、雨后有彩虹9. 如图,在△ABC中,∠ABC,∠ACB的平分线交于点D,过点D作EF∥BC交AB于点E,交AC于点F.若AB=12,AC=8,BC=10,则△AEF的周长是( )
8. 下列事件中,是确定事件的是( )A、古筝弹得好歌就唱得好 B、昨天太阳从西边升起 C、网红看过电影《少年的你》 D、雨后有彩虹9. 如图,在△ABC中,∠ABC,∠ACB的平分线交于点D,过点D作EF∥BC交AB于点E,交AC于点F.若AB=12,AC=8,BC=10,则△AEF的周长是( )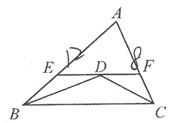 A、15 B、18 C、20 D、2210. 若等腰三角形的底角为15°,则一腰上的高是腰长的( )A、 B、 C、1倍 D、2倍11. 从1,3,-5,7中任取一数,记为m,使x2+(m+1)x+16为完全平方式的概率是( )A、 B、 C、 D、112. 如图,△ABC和△BDE都是等边三角形,点A,B,D在一条直线上。给出4个结论:①AE=CD;②AB⊥FB;③∠AFC=60°;④△BGH是等边三角形。其中正确的是( )
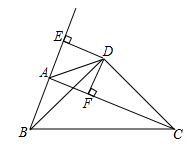
A、15 B、18 C、20 D、2210. 若等腰三角形的底角为15°,则一腰上的高是腰长的( )A、 B、 C、1倍 D、2倍11. 从1,3,-5,7中任取一数,记为m,使x2+(m+1)x+16为完全平方式的概率是( )A、 B、 C、 D、112. 如图,△ABC和△BDE都是等边三角形,点A,B,D在一条直线上。给出4个结论:①AE=CD;②AB⊥FB;③∠AFC=60°;④△BGH是等边三角形。其中正确的是( )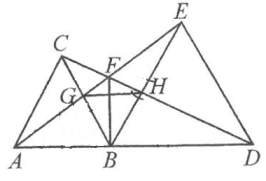 A、①,②,③ B、①,②,④ C、①,③,④ D、②,③,④
A、①,②,③ B、①,②,④ C、①,③,④ D、②,③,④二、填空题:本题共4小题,每小题3分,共12分.
-
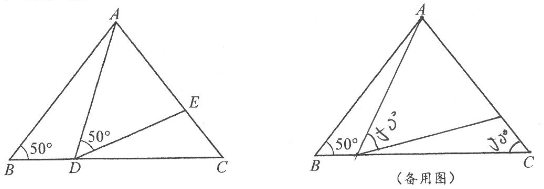
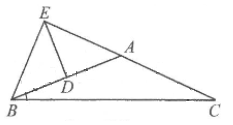
13. 两条平行线被第三条直线所截,一对内错角的角平分线的位置关系是.14. 给出4个事件:①任意画一个三角形,其内角和是90°;②袋中装有3个黑球、6个白球(这些球除颜色外都相同),随机摸出一个球,恰好是白球;③掷一枚质地均匀的骰子(六个而上分别刻有1到6的点数),向上一面的点数恰好为偶数;④任意画一个扇形、恰好是轴对称图形,按发生的可能性从小到大排列,事件的序号依次是.15. 如图,在△ABC中,AB=AC,AB的垂直平分线DE交CA的延长线于点E,垂足为D,∠CBE=69°.则∠C=°.
 16. 如图,将纸板四周突起部分折起,可制成高为a的长方体形状的无盖纸盒.若纸盒的容积为4a2b,底面长方形的一边长为b,则纸板的面积是.
16. 如图,将纸板四周突起部分折起,可制成高为a的长方体形状的无盖纸盒.若纸盒的容积为4a2b,底面长方形的一边长为b,则纸板的面积是.
三、解答题:本题共7小题,共52分.解答应写出文字说明、证明过程或演算步骤。
-
17. 计算:(1)、102×100÷10-1;(2)、(x+2)2-(x+1)(x-1).18. 声音在空气中的传播速度y(m/s)随气温x(℃)的变化而变化.下表给出了一组不同气温下声音传播的速度:
x(℃)
0
5
10
15
20
25
y(m/s)
331
334
337
340
343
346
(1)、当x的值为35时,求对应的y的值;(2)、求y与x的关系式.19. 如图,∠1=∠2,AB=AD,点E在边BC上,∠C=∠AED,AB与DE交于点O.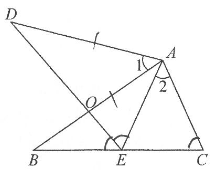 (1)、求证:△ABC≌△ADE;(2)、当∠1=40°时,求∠BED的度数.20. 如图
(1)、求证:△ABC≌△ADE;(2)、当∠1=40°时,求∠BED的度数.20. 如图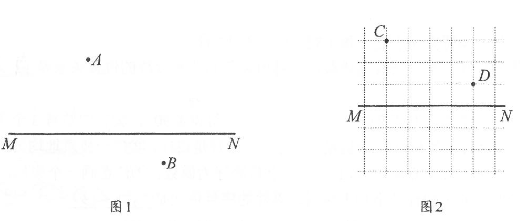 (1)、如图1,学校A,B在道路MN的异侧.在MN上建公交站P,使得P到A,B的距离相等。利用尺规作图确定P的位置.(2)、如图2,学校C,D在道路MN的同侧,在MN上建公交站Q,使得Q到C,D的距离的和最短.利用网格确定Q的位置.21. 尺规作图:作点A关于直线l的对称点A'.
(1)、如图1,学校A,B在道路MN的异侧.在MN上建公交站P,使得P到A,B的距离相等。利用尺规作图确定P的位置.(2)、如图2,学校C,D在道路MN的同侧,在MN上建公交站Q,使得Q到C,D的距离的和最短.利用网格确定Q的位置.21. 尺规作图:作点A关于直线l的对称点A'.已知:直线l和l外一点A.
求作:点A关于l的对称点A'.
作法:①在l上任取一点P,以点P为圆心,PA长为半径作孤,交l于点B;②以点B为圆心,AB长为半径作弧,交弧AB于点A'. 点A'就是所求作的对称点.
由步骤①,得
由步骤②,得
将横线上的内容填写完整,并说明点A与A'关于直线l对称的理由.