河北省石家庄市赵县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2019-07-24 类型：期末考试

进入出卷网下载

一、选择题(每小题3分，共45分)

1. 下列二次根式中，最简二次根式的个数有（）
① $\sqrt{0.2}$ ② $\sqrt{3 a}$ (a>0)③ $\sqrt{a^{2} + b^{2}}$ ④ $\sqrt{\frac{2}{5}}$

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 若代数式 $\frac{\sqrt{x - 2}}{\sqrt{x - 1}}$ 有意义则实数x的取值范围是（）

A、x≥1 B、x≥2 C、x＞0 D、x＞2

查看试题解析
3. 已知△ABC的三边之长分别为a、1、3，则化简|9-2a|- $\sqrt{9 - 12 a + 4 a^{2}}$ 的结果是（）

A、12-4a B、4a-12 C、12 D、-12

查看试题解析
4. 下列几组数中，是勾股数的有（）
①5、12、13②13、1415③3k、4k、5k(k为正整数)④ $\frac{2}{3}$ 、2、 $\frac{7}{3}$

A、1组 B、2组 C、3组 D、4组

查看试题解析
5. 将一根长24cm的筷子置于底面直径为5cm，高为12cm的圆柱水杯中，设筷子露在杯子外面的长度为h，则h的取值范围是（）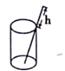

A、12cm≤h≤19cm B、12cm≤h≤13cm C、11cm≤h≤12cm D、5cm≤h≤12cm

查看试题解析
6. 在直线l上有三个正方形m、q、n，若m、q的面积分别为5和11，则n的面积（）

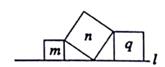A、4 B、6 C、16 D、55

查看试题解析
7. 在正方形ABCD中，E、F是对角线AC上两点连接BE、BF、DE、DF，则A添加下列哪一个条件可以判定四边形BEDF是菱形（）

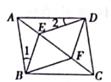A、∠1=∠2 B、BE=DF C、∠EDF=60° D、AB=AF

查看试题解析
8. 在平行四边形中按以下步骤作图：(1)分别以A、B为圆心，以大于 $\frac{1}{2}$ AB为半径画弧，两弧相交于PQ两点；(2)连接PQ分别交AB、CD于E、F两点；(3)连接AE、BE若DC=5、EF=3，则△AEB的面积为（）

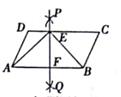A、15 B、 $\frac{15}{2}$ C、8 D、10

查看试题解析
9. 在菱形ABCD中，M、N分别在AB、CD上，且AM=CN，MN与AC交于点O，连Q接BO，若∠DAC=62°，则∠OBC的度数为（）

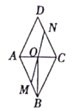A、28° B、52° C、62° D、72°

查看试题解析
10. 八年级(6)班一同学感冒发烧住院治疗，护士为了较直观地了解这位同学这天24h的体温和时间的关系，可选择的比较好的方法是（）

A、列表法 B、图象法 C、解析式法 D、以上三种方法均可

查看试题解析
11. 把直线y=-x+3向上平移m个单位长度后，与直线y=2x+4的交点在第一象限，则m的取值范围是（）

A、1＜m<7 B、3<m<4 C、m＞1 D、m＜4

查看试题解析
12. 以下所给四幅图象近似刻画了两个变量之间的关系，请按图象顺序将下面四种情景与之对应排序为（）
①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)②向下宽上窄的容器中匀速注水(水面的高度与注水时间的关系)③将常温下的温度计插入一杯热水中(温度计读数与时间关系)④一杯越来越凉的水(水温与时间的关系)

A、①②③④ B、③④②① C、①④②③ D、③②④①

查看试题解析
13. 若一组数据1，2，3，4，x的平均数与中位数相同，则实数x的值不可能是（　　）

A、0 B、2.5 C、3 D、5

查看试题解析
14. 如图，直线y₁=mx经过P(2，1)和Q(-4，-2)两点，且与直线y₂=kx+b交于点P，则不等式kx+b>mx的解集为（）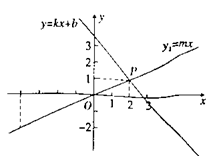

A、x>2 B、x<2 C、x>-4 D、x<-4

查看试题解析
15. 某校规定：学生的平时作业，期中考试期末考试三项成绩分别是按30%、30%40%计入学期总评成绩，小明的平时作业，期中考试期末考试的英语成绩分别是93分、90分、96分；则小明这学期的总评成绩是（）

A、92 B、90 C、93 D、93.3

查看试题解析

二、填空题(每小题3分，共15分)

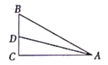
16. 若直角三角形两边的长分别为a、b且满足 $\sqrt{a^{2} - 10 a + 25}$ +|b-4|=0，则第三边的长是。

查看试题解析
17. 在Rt△ABC中，∠ACB=90°，AD平分∠BAC与BC相交于点D，若BD=2，CD=1，则AC的长是。

查看试题解析
18. 若直线l₁与l₂相交于点P，则根据图象可得二元一次方程组 ${\begin{cases} 2 x - y = 3 \\ x + y = 3 \end{cases}$ 的解是。

查看试题解析
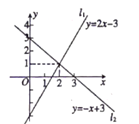19. 在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD=BC，∠EPF=147°，则∠PFE的度数是。

查看试题解析
20. 观察下列等式
第1个等式：a₁= $\frac{1}{1 + \sqrt{2}}$ = $\sqrt{2}$ -1，第2个等式：a₂= $\frac{1}{\sqrt{2} + \sqrt{3}}$ = $\sqrt{3}$ - $\sqrt{2}$ ，

第3个等式：a₃= $\frac{1}{\sqrt{3} + 2}$ =2- $\sqrt{3}$ ，第4个等式：a₄₌ $\frac{1}{2 + \sqrt{5}}$ = $\sqrt{5}$ -2

按上述规律，第n个等式为a_n= ，那么a₁+a₂+…a_n= ．

查看试题解析

三、解答题(共60分)

21. 计算:

(1)、(3 $\sqrt{12}$ -2 $\sqrt{\frac{1}{3}}$ + $\sqrt{48}$ )÷2 $\sqrt{3}$

(2)、( $\sqrt{3}$ -1)²+( $\sqrt{3}$ +2)²-2( $\sqrt{3}$ -1)( $\sqrt{3}$ +2)

(3)、先化简:再求值．
$(\frac{a - b}{a^{2} - 2 a b + b^{2}} - \frac{a}{a^{2} - 2 a b}) \div \frac{b}{a - 2 b}$ ，其中a=2 $\sqrt{2}$ ，b= $\sqrt{2}$

查看试题解析
22. 在△ABC中，AD是BC边上的高，CE是AB边上的中线，且∠B=2∠BCE，求证DC=BE。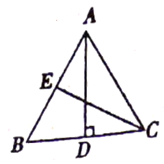

查看试题解析
23. 随着移动互联网的快速发展，基于互联网的共享单车应运而生，为了解某小区居民使用共享单车的情况，某研究小组随机采访该小区的10位居民，得到这10位居民，一周内使用共享单车的次数分别是:17、12、15、20、17、0、7、26、17、9

(1)、这组数据的中位数是，众数是。

(2)、计算这10位居民一周内使用共享单车的平均次数

(3)、若该小区有200名居民，试估计该小区居民一周内使用共享单车的总次数。

查看试题解析
24. 勾股定理神秘而美妙，它的证法多样，其中的“面积法”给了李明灵感，他惊喜地发现：当两个全等的直角三角形如图(1)摆放时可以利用“面积法”来证明勾股定理，过程如下：
如图(1)∠DAB=90求证：a²+b²=c²

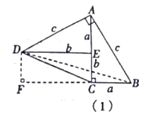
证明：连接DB，过点D作DF⊥BC交BC的延长线于点F，则DF=b-a

∵S_{四边形ADCB}=S_△AD_C+S_△_ABC= $\frac{1}{2}$ b²+ $\frac{1}{2}$ ab

S_{四边形ADCB}=S_△_ADB+S_△_BCD= $\frac{1}{2}$ c²+ $\frac{1}{2}$ a(b-a)

∴ $\frac{1}{2}$ b²+ $\frac{1}{2}$ ab= $\frac{1}{2}$ c²+ $\frac{1}{2}$ a(b-a)

化简得：a²+b²=c²

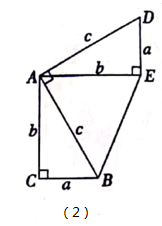
请参照上述证法，利用“面积法”完成如图(2)的勾股定理的证明：

如图(2)中∠DAB=90°，求证：a₂+b²=c²

查看试题解析
25. 已知：如图在菱形ABCD中，AB=4，∠DAB=30°，点E是AD的中点，点M是AB边上的一个动点(不与点A重合)，连接ME并延长交CD的延长线于点N，连接MD、AN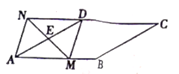

(1)、求证：四边形AMDN是平行四边形。

(2)、当AM为何值时，四边形AMDN是矩形，并说明理由。

查看试题解析
26. “五一”假期某商场某运动品牌服装专卖店，准备购进甲、乙两种服装，甲种服装每件进价180元，售价320元;乙种服装每件进价150元售价280元

(1)、若该专卖店同时购进甲、乙两种服装共200件，恰好用去32400元，购进甲、乙两种服装各多少件?

(2)、该专卖店为使甲、乙两种服装共200件的总利润利润=售价-进价)不少于26700元，且不超过26800元，则该专卖店有几种进货方案?

(3)、在(2)的条件下，该专卖店准备在5月1日当天对甲种服装进行优惠促销活动决定对甲种服装每件优惠a(0<a<20)元出售，乙种服装价格不变，那么该专卖店要获得最大利润应如何进货?

查看试题解析