四川省乐山市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-07-24 类型:期末考试
一、选择题:本大题共12小题,每小题3分,共36分
-
1. 一种微粒的半径是4×10-5米,用小数表示为( )A、0.0000004米 B、0.000004米 C、0.00004米 D、0.0004米2. 分式 可变形为( )A、 B、 C、 D、3. 若点P(2m-1,1)在第二象限,则m的取值范围是( )A、m< B、m> C、m≤ D、m≥4. 四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )A、AB=CD B、AB=BC C、AC⊥BD D、AC=BD5. 老师在计算学生每学期的总成绩时,是把平时成绩和考试成绩按如图所示的比例计算.如果一个学生的平时成绩为70分,考试成绩为90分,那么他的学期总评成绩应为( )
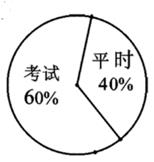 A、70分 B、90分 C、82分 D、80分6. 如图,在 ABCD中,∠BAC=78°,∠ACB=38°,则∠D的度数是( )
A、70分 B、90分 C、82分 D、80分6. 如图,在 ABCD中,∠BAC=78°,∠ACB=38°,则∠D的度数是( )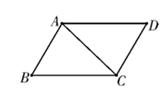 A、52° B、64° C、78° D、38°7. 一次函数y=kx+b(k<0,b>0)的图象可能是( )A、
A、52° B、64° C、78° D、38°7. 一次函数y=kx+b(k<0,b>0)的图象可能是( )A、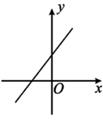 B、
B、 C、
C、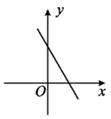 D、
D、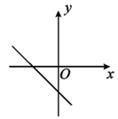 8. 如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF=2,则菱形ABCD的边长为( )
8. 如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF=2,则菱形ABCD的边长为( )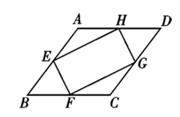 A、 B、2 C、2 D、49. 将直线y=-2x向上平移5个单位,得到的直线的解析式为( )A、y=-2x-5 B、y=-2x+5 C、y=-2(x-5) D、y=-2(x+5)10. 如图,在▱ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于( )
A、 B、2 C、2 D、49. 将直线y=-2x向上平移5个单位,得到的直线的解析式为( )A、y=-2x-5 B、y=-2x+5 C、y=-2(x-5) D、y=-2(x+5)10. 如图,在▱ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于( ) A、8cm B、6cm C、4cm D、2cm11. 如图,四边形ABCD是菱形,AC=8,BD=6,DH⊥AB于H,则DH=( )
A、8cm B、6cm C、4cm D、2cm11. 如图,四边形ABCD是菱形,AC=8,BD=6,DH⊥AB于H,则DH=( )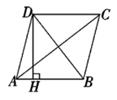 A、 B、 C、12 D、2412. 如图,点A、B在反比例函数y= (x>0)的图象上,点C、D在反比例函数y= (x>0)的图象上,AC∥BD∥y轴,已知点A、B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )
A、 B、 C、12 D、2412. 如图,点A、B在反比例函数y= (x>0)的图象上,点C、D在反比例函数y= (x>0)的图象上,AC∥BD∥y轴,已知点A、B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )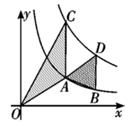 A、4 B、3 C、2 D、
A、4 B、3 C、2 D、二、填空题:本大题共6小题,每小题3分,共18分.
-
13. 使分式 有意义的x的范围是 。14. 数据-2,-1,0,1,2,4的中位数是 。15. 一次函数y=2x-6的图象与坐标轴围成的三角形面积为 。16. 如图,在 ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC= 。
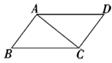 17. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
17. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 . (把你认为正确说法的序号都填上)
 18. 已知△ABC的三个顶点为A(-1,1),B(-1,3),C(-3,-3),将△ABC向右平移m(m>0)个单位后,△ABC某一边的中点恰好落在反比例函数y= 的图象上,则m的值为。
18. 已知△ABC的三个顶点为A(-1,1),B(-1,3),C(-3,-3),将△ABC向右平移m(m>0)个单位后,△ABC某一边的中点恰好落在反比例函数y= 的图象上,则m的值为。
三、本大题包含第19题、20题、21题,共3小题,每小题8分,共24分.
-
19. 计算:(- )2×( )-2+(-2019)020. 解方程: .21. 如图,AC为矩形ABCD的对角线,DE⊥AC于E,BF⊥AC于F。
求证:DE=BF
四、本大题包含第22题、23题、24题,共3小题,每小题9分,共27分
-
22. 先化简,再求值: ,其中x=23. 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y= 在第一象限的图象分别交OA、AB于点C、D,且S△BOD=4
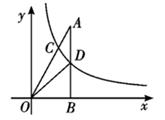 (1)、求反比例函数的表达式;(2)、求点C的坐标24. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
(1)、求反比例函数的表达式;(2)、求点C的坐标24. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图: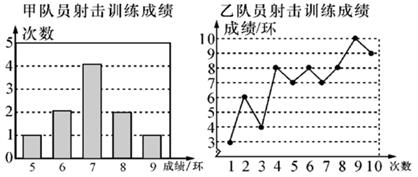
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)、求表格中a,b,c的值(2)、分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?五、本大题包含第25题、26题,共2小题,每小题10分,共20分
-
25. 如图,将 ABCD的AD边延长至点E,使DE= AD连结CE,F是BC边的中点,连结FD
 (1)、求证:四边形CEDF是平行四边形;(2)、若AB=3,AD=4,∠A=60°,求CE的长26. 如图,已知直线l1:y=-2x+4与x、y轴分别交于点N、C,与直线l2:y=kx+b(k≠0)交于点M,点M的横坐标为1,直线l2与x轴的交点为A(-2,0)
(1)、求证:四边形CEDF是平行四边形;(2)、若AB=3,AD=4,∠A=60°,求CE的长26. 如图,已知直线l1:y=-2x+4与x、y轴分别交于点N、C,与直线l2:y=kx+b(k≠0)交于点M,点M的横坐标为1,直线l2与x轴的交点为A(-2,0)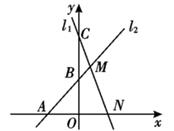 (1)、求k,b的值;(2)、求四边形MNOB的面积.
(1)、求k,b的值;(2)、求四边形MNOB的面积.六、本大题共2小题,第27题12分,第28题13分,共25分.
-
27. 如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF.连结DE,过点E作EG⊥DE,使EG=DE,连结FG、FC
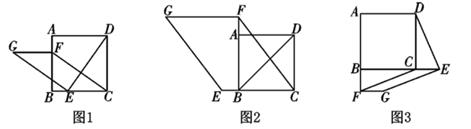 (1)、请判断:FG与CE的数量关系是 , 位置关系是 。(2)、如图2,若点E、F分别是边CB、BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;(3)、如图3,若点E、F分别是边BC、AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断。28. 如图,四边形ABCD的四个顶点分别在反比例函数y= 与y= (x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4
(1)、请判断:FG与CE的数量关系是 , 位置关系是 。(2)、如图2,若点E、F分别是边CB、BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;(3)、如图3,若点E、F分别是边BC、AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断。28. 如图,四边形ABCD的四个顶点分别在反比例函数y= 与y= (x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4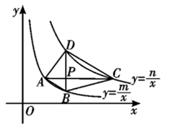 (1)、当m=4,n=20时
(1)、当m=4,n=20时①若点P的纵坐标为2,求直线AB的函数表达式
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由
(2)、四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.