黑龙江省绥化市2019年中考数学试卷
试卷更新日期:2019-07-24 类型:中考真卷
一、单项选择题(本题共10个小题,每小题3分,共30分)
-
1. 我们的祖国地域辽阔,其中领水面积约为37000km2.把370000这个数用科学记数
法表示为( )
A、37×104 B、3.7×105 C、0.37×106 D、3.7×1062. 下列图形中,属于中心对称图形的是( )A、 B、
B、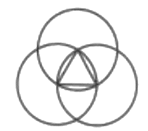 C、
C、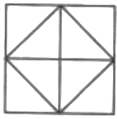 D、
D、 3. 下列计算正确的是( )A、 =±3 B、(-1)0=0 C、 D、 =24. 若一个几何体的主视图、俯视图、左视图都是半径相等的圆,则这个几何体是( )A、球体 B、圆锥 C、圆柱 D、正方体5. 下列因式分解正确的是( )A、x2-x=x(x+1) B、a2-3a-4=(a+4)(a-1) C、a2+2ab-b2=(a-b)2 D、x2-y2=(x+y)(x-y)6. 不透明袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是( )A、 B、 C、 D、7. 下列命题是假命题的是( )A、三角形两边的和大于第三边 B、正六边形的每个中心角都等于60° C、半径为R的圆内接正方形的边长等于 R D、只有正方形的外角和等于360°8. 小明去商店购买A、B两种玩具,共用了10元钱,A种玩具每件1元,B种玩具每件2元.若每种玩具至少买一件,且A种玩具的数量多于B种玩具的数量.则小明的购买方案有( )A、5种 B、4种 C、3种 D、2种9. 不等式组 的解集在数轴上表示正确的是( )A、
3. 下列计算正确的是( )A、 =±3 B、(-1)0=0 C、 D、 =24. 若一个几何体的主视图、俯视图、左视图都是半径相等的圆,则这个几何体是( )A、球体 B、圆锥 C、圆柱 D、正方体5. 下列因式分解正确的是( )A、x2-x=x(x+1) B、a2-3a-4=(a+4)(a-1) C、a2+2ab-b2=(a-b)2 D、x2-y2=(x+y)(x-y)6. 不透明袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是( )A、 B、 C、 D、7. 下列命题是假命题的是( )A、三角形两边的和大于第三边 B、正六边形的每个中心角都等于60° C、半径为R的圆内接正方形的边长等于 R D、只有正方形的外角和等于360°8. 小明去商店购买A、B两种玩具,共用了10元钱,A种玩具每件1元,B种玩具每件2元.若每种玩具至少买一件,且A种玩具的数量多于B种玩具的数量.则小明的购买方案有( )A、5种 B、4种 C、3种 D、2种9. 不等式组 的解集在数轴上表示正确的是( )A、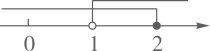 B、
B、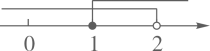 C、
C、 D、
D、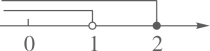 10. 如图,在正方形ABCD中,E、F是对角线AC上的两个动点,P是正方形四边上的任意一点,且AB=4,EF=2,设AE=x.当△PEF是等腰三角形时,下列关于P点个数的说法中,一定正确的是( )
10. 如图,在正方形ABCD中,E、F是对角线AC上的两个动点,P是正方形四边上的任意一点,且AB=4,EF=2,设AE=x.当△PEF是等腰三角形时,下列关于P点个数的说法中,一定正确的是( )
①当x=0(即E、A两点重合)时,P点有6个②当0<x<4 -2时,P点最多有9个③当P点有8个时,x=2 -2④当△PEF是等边三角形时,P点有4个
A、①③ B、①④ C、②④ D、②③二、填空题(本题共11个小题,每小题3分,共33分)
-
11. 某年一月份,哈尔滨市的平均气温约为-20℃,绥化市的平均气温约为-23℃,则两地的温差为 ℃.12. 若分式 有意义,则x的取值范围是 。13. 计算:(-m3)2÷m4=。14. 已知一组数据1,3,5,7,9,则这组数据的方差是。15. 当a=2018时,代数式 的值是 。
16. 用一个圆心角为120°的扇形作一个圆锥的侧面,若这个圆锥的底面半径恰好等于4,则这个圆锥的母线长为 。17. 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A= 度。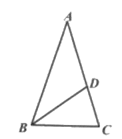 18. 一次函数y1=-x+6与反比例函数y2= (x>0)的图象如图所示当y1>y2时,自变量x的取值范围是 。
18. 一次函数y1=-x+6与反比例函数y2= (x>0)的图象如图所示当y1>y2时,自变量x的取值范围是 。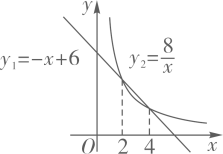 19. 甲、乙两辆汽车同时从A地出发,开往相距200km的B地,甲、乙两车的速度之比是4:5,结果乙车比甲车早30分钟到达B地,则甲车的速度为 km/h.20. 半径为5的⊙O是锐角三角形ABC的外接圆,AB=AC,连接OB,OC,延长CO交弦AB于点D.若△OBD是直角三角形,则弦BC的长为 .21. 在平面直角坐标系中,若干个边长为1个单位长度的等边三角形,按下图中的规律摆放点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“OA1→A1A2→A2A3→A3A4→A4A3…”的路线运动设第n秒运动到点P(n为正整数),则点P2019的坐标是 .
19. 甲、乙两辆汽车同时从A地出发,开往相距200km的B地,甲、乙两车的速度之比是4:5,结果乙车比甲车早30分钟到达B地,则甲车的速度为 km/h.20. 半径为5的⊙O是锐角三角形ABC的外接圆,AB=AC,连接OB,OC,延长CO交弦AB于点D.若△OBD是直角三角形,则弦BC的长为 .21. 在平面直角坐标系中,若干个边长为1个单位长度的等边三角形,按下图中的规律摆放点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“OA1→A1A2→A2A3→A3A4→A4A3…”的路线运动设第n秒运动到点P(n为正整数),则点P2019的坐标是 .
三、解答题(本题共8个小题,共57分)
-
22. 如图,已知△ABC三个顶点的坐标分别为A(-2,-4),B(0,-4),C(1,-1)
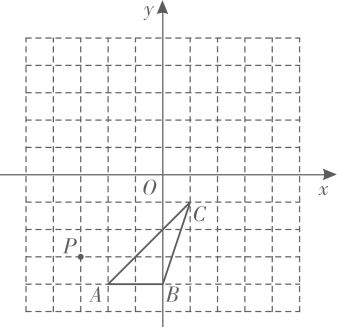 (1)、请在网格中,画出线段BC关于原点对称的线段B1C1:(2)、请在网格中,过点C画一条直线CD,
(1)、请在网格中,画出线段BC关于原点对称的线段B1C1:(2)、请在网格中,过点C画一条直线CD,将△ABC分成面积相等的两部分,与线段AB相交于点D,写出点D的坐标
(3)、若另有一点P(-3,-3),连接PC,则tan∠BCP= 。23. 小明为了了解本校学生的假期活动方式,随机对本校的部分学生进行了调查收集整理数据后,小明将假期活动方式分为五类:A.读书看报;B.健身活动:C.做家务D.外出游玩:E.其他方式,并绘制了不完整的统计图如下.统计后发现“做家务”的学生人数占调查总人数的20%请根据图中的信息解答下列问题
 (1)、本次调查的总人数是人;(2)、补全条形统计图;(3)、根据调查结果,估计本校2360名学生中“假期活动方式”是“读书看报”的有多少人?24. 按要求解答下列各题:
(1)、本次调查的总人数是人;(2)、补全条形统计图;(3)、根据调查结果,估计本校2360名学生中“假期活动方式”是“读书看报”的有多少人?24. 按要求解答下列各题: (1)、如图①,求作一点P,使点P到∠ABC的两边的距离相等,且在△ABC的边AC上.(用直尺和圆规作图,保留作图痕迹,不写作法和证明)(2)、如图②,B、C表示两个港口,港口C在港口B的正东方向上海上有一小岛A在港口B的北偏东60°方向上,且在港口C的北偏西45°方向上测得AB=40海里,求小岛A与港口C之间的距离.(结果可保留根号)25. 已知关于x的方程kx2-3x+1=0有实数根(1)、求k的取值范围(2)、若该方程有两个实数根,分别为x1和x2,当x1+x2+x1x2=4时,求k的值26. 如图,AB为⊙O的直径,AC平分∠BAD,交弦BD于点G,连接半径OC交BD于点E,过点C的一条直线交AB的延长线于点F,∠AFC=∠ACD
(1)、如图①,求作一点P,使点P到∠ABC的两边的距离相等,且在△ABC的边AC上.(用直尺和圆规作图,保留作图痕迹,不写作法和证明)(2)、如图②,B、C表示两个港口,港口C在港口B的正东方向上海上有一小岛A在港口B的北偏东60°方向上,且在港口C的北偏西45°方向上测得AB=40海里,求小岛A与港口C之间的距离.(结果可保留根号)25. 已知关于x的方程kx2-3x+1=0有实数根(1)、求k的取值范围(2)、若该方程有两个实数根,分别为x1和x2,当x1+x2+x1x2=4时,求k的值26. 如图,AB为⊙O的直径,AC平分∠BAD,交弦BD于点G,连接半径OC交BD于点E,过点C的一条直线交AB的延长线于点F,∠AFC=∠ACD (1)、求证:直线CF是⊙O的切线(2)、若DE=2CE=2.
(1)、求证:直线CF是⊙O的切线(2)、若DE=2CE=2.①求AD的长
②求△ACF的周长.(结果可保留根号)
27. 甲、乙两台机器共同加工一批零件,一共用了6小时,在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工甲机器在加工过程中工作效率保持不变。甲、乙两台机器加工零件的总数y(个)与甲加工时间x)之间的函数图象为折线 OA-AB-BC,如图所示。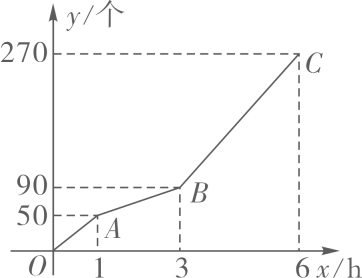 (1)、这批零件一共有 个,甲机器每小时加工个零件,乙机器排除故障后每小时加工个零件;(2)、当3≤x≤6时,求y与x之间的函数解析式;(3)、在整个加工过程中,甲加工多长时间时,甲与乙加工的零个数相等?28. 如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N
(1)、这批零件一共有 个,甲机器每小时加工个零件,乙机器排除故障后每小时加工个零件;(2)、当3≤x≤6时,求y与x之间的函数解析式;(3)、在整个加工过程中,甲加工多长时间时,甲与乙加工的零个数相等?28. 如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N (1)、求证:MN=MC;(2)、若DM:DB=2:5,求证:AN=4BN;(3)、如图②,连接MC交BD于点G.若BG:MG=3:5,求NG·CG的值29. 已知抛物线y=ax2+bx+3的对称轴为直线x= ,交x轴于点A、B,交y轴于点C,且点A坐标为A(-2,0),直线y=-mx-n(m>0)与抛物线交于点P、Q(点P在点Q的右边),交y轴于点H
(1)、求证:MN=MC;(2)、若DM:DB=2:5,求证:AN=4BN;(3)、如图②,连接MC交BD于点G.若BG:MG=3:5,求NG·CG的值29. 已知抛物线y=ax2+bx+3的对称轴为直线x= ,交x轴于点A、B,交y轴于点C,且点A坐标为A(-2,0),直线y=-mx-n(m>0)与抛物线交于点P、Q(点P在点Q的右边),交y轴于点H (1)、求该抛物线的解析式(2)、若n=5,且△CPQ的面积为3,求m的值(3)、当m≠1时,若n=-3m,直线AQ交y轴于点K.设△PQK的面积为S,求S与m之间的函数解析式。
(1)、求该抛物线的解析式(2)、若n=5,且△CPQ的面积为3,求m的值(3)、当m≠1时,若n=-3m,直线AQ交y轴于点K.设△PQK的面积为S,求S与m之间的函数解析式。