广东省肇庆市封开县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-07-24 类型:期末考试
一、选择题(本大题10小题,每小题3分,共30分)
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 下列四组线段中,可以构成直角三角形的是( )A、4,5,6 B、2,3,4 C、1,1, D、1, ,33. 某班5位学生参加中考体育测试的成绩(单位:分)分别是:50、45、36、48、50,则这组数据的众数是( )A、36 B、45 C、48 D、504. 下列计算正确的是( )A、 B、 C、 D、5. 已知正比例函数y=3x的图象经过点(1,m),则m的值为( )A、 B、 C、3 D、-36. 若代数式 有意义,则实数x的取值范围是( )A、x≠-3 B、x>-3 C、x≥-3 D、任意实数7. 如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是24cm,那么△DEF的周长是( )
 A、6cm B、12cm C、18cm D、32cm8. 如图,菱形ABCD中,∠ABC=60°,AB=6,则BD=( )
A、6cm B、12cm C、18cm D、32cm8. 如图,菱形ABCD中,∠ABC=60°,AB=6,则BD=( )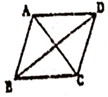 A、 B、 C、 D、9. 已知四边形ABCD是平行四边形,下列结论中不正确的是( )A、当AB=BC时,四边形ABCD是菱形 B、当AC=BD时,四边形ABCD是正方形 C、当AC⊥BD时,四边形ABCD是菱形 D、当∠ABC=90°时,四边形ABCD是矩形10. 若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是( )A、
A、 B、 C、 D、9. 已知四边形ABCD是平行四边形,下列结论中不正确的是( )A、当AB=BC时,四边形ABCD是菱形 B、当AC=BD时,四边形ABCD是正方形 C、当AC⊥BD时,四边形ABCD是菱形 D、当∠ABC=90°时,四边形ABCD是矩形10. 若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是( )A、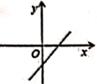 B、
B、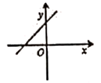 C、
C、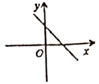 D、
D、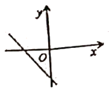
二、填空题(本大题6小题,每小题4分,共24分)
-
11. 化简:=12. 一次函数y=2x-6的图像与x轴的交点坐标为 .13. 在△ABC中,∠C=90°,若b=7;c=9,则a= ,14. 正比例函数y=kx的图象与直线对y=-x+1线交于的点P(a,2),则k的值是 .
15. 如图,点O是矩形ABCD的对角线AC的中点,M是AD的中点,若OM=3,BC=8,则OB的长为 。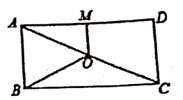 16. 如图,在平行四边形ABCD中,∠ABC的平分线BF交AD于点F,FE∥AB.若AB=5,BF=6,则四边形ABEF的面积为 。
16. 如图,在平行四边形ABCD中,∠ABC的平分线BF交AD于点F,FE∥AB.若AB=5,BF=6,则四边形ABEF的面积为 。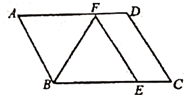
三、解答题(一)(本大题3小题,每小题6分,共18分)
-
17. 计算:18. 在△ABC中,∠ABC=90°,
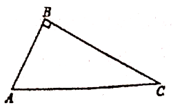 (1)、作线段AC的垂直平分线l,交AC于点O;(保留作图痕迹,请标明字母);(2)、连接BO并延长至D,使得OD=OB;连接DA、DC,证明四边形ABCD是矩形。19. 某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
(1)、作线段AC的垂直平分线l,交AC于点O;(保留作图痕迹,请标明字母);(2)、连接BO并延长至D,使得OD=OB;连接DA、DC,证明四边形ABCD是矩形。19. 某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题: (1)、本次调查的学生人数为 ,如乐节 在扇形统计图中所占圆心角的度数是度。(2)、请将条形统计图补充完整;(3)、若该中学有2000名学生,请估计该校喜爱动画节目的人数
(1)、本次调查的学生人数为 ,如乐节 在扇形统计图中所占圆心角的度数是度。(2)、请将条形统计图补充完整;(3)、若该中学有2000名学生,请估计该校喜爱动画节目的人数四、解答题(二)(本大题3小题,每小题7分,共21分)
-
20. 先化简,再求值: ,其中x=2+21. 已知直线y=x+b分别交x轴于点A、交y轴于点B(0,2).(1)、求该直线的函数表达式;(2)、求线段AB的长.22. 如图,在四边形ABCD中,AB∥CD,AC、BD相交于点O,且O是BD的中点
 (1)、求证:四边形ABCD是平行四边形;(2)、若AC⊥BD,AB=8,求四边形ABCD的周长
(1)、求证:四边形ABCD是平行四边形;(2)、若AC⊥BD,AB=8,求四边形ABCD的周长五、解答题(三)(本大题3小题,每小题9分,共27分)
-
23. 如图,已知直线y=k+b交x轴于点A,交y轴于点B,直线y=2x-4交x轴于点D,与直线AB相交于点C(3,2)
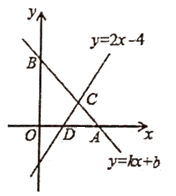 (1)、根据图象,写出关于x的不等式2x-4>kx+b的解集(2)、若点A的坐标为(5,0),求直线AB的解析式;(3)、在(2)的条件下,求四边形BODC的面积。24. 在Rt△ABC与R△ABD中,∠ABC=∠BAD=90°,AC=BD,AC、B相交于作点G,过点交A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE、BF相交于点H,
(1)、根据图象,写出关于x的不等式2x-4>kx+b的解集(2)、若点A的坐标为(5,0),求直线AB的解析式;(3)、在(2)的条件下,求四边形BODC的面积。24. 在Rt△ABC与R△ABD中,∠ABC=∠BAD=90°,AC=BD,AC、B相交于作点G,过点交A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE、BF相交于点H, (1)、证明:△ABD≌△BAC(2)、证明:四边形AHBG是菱形(3)、若AB=BC,证明四边形AHBG是正方形.的25. 已知:如图,四边形ABCD为矩形,AB=10,BC=3,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,设运动时间为t秒。
(1)、证明:△ABD≌△BAC(2)、证明:四边形AHBG是菱形(3)、若AB=BC,证明四边形AHBG是正方形.的25. 已知:如图,四边形ABCD为矩形,AB=10,BC=3,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,设运动时间为t秒。 (1)、当点P在线段AB上运动了t秒时,BP=(用代数式表示);(2)、t为何值时,四边形PDEB是平行四边形(3)、在直线AB上是否存在点Q,使以D、E、Q、P四点为顶点的四边形是菱形,若存在,求出t的值,若不存在,说明理由。
(1)、当点P在线段AB上运动了t秒时,BP=(用代数式表示);(2)、t为何值时,四边形PDEB是平行四边形(3)、在直线AB上是否存在点Q,使以D、E、Q、P四点为顶点的四边形是菱形,若存在,求出t的值,若不存在,说明理由。