河北省衡水市景县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-24 类型:期末考试
一、选择题(本大题共14个小题每小题3分共42分)
-
1. 4的平方根是( )
A、2 B、-2 C、±2 D、162. 如图1,在平面直角坐标系中,点P的坐标为( )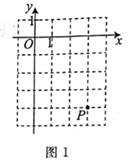 A、(3,-4) B、(-4,3) C、(-3,4) D、(4,-3)3. 在下列调查中,不宜选择全面调查方式的是( )A、为了了解某班学生“50米跑”的成绩 B、为了了解一个班学生的睡眠情况 C、为了检测某城市的空气质量 D、为了了解神舟飞船的设备零件的质量情况4. 如图,两条直线相交于点O,OE⊥AB,∠1=56°,则∠2等于( )
A、(3,-4) B、(-4,3) C、(-3,4) D、(4,-3)3. 在下列调查中,不宜选择全面调查方式的是( )A、为了了解某班学生“50米跑”的成绩 B、为了了解一个班学生的睡眠情况 C、为了检测某城市的空气质量 D、为了了解神舟飞船的设备零件的质量情况4. 如图,两条直线相交于点O,OE⊥AB,∠1=56°,则∠2等于( ) A、44° B、56° C、45° D、34°5. 已知一组数据 ,π, ,0.0456, ,1.010010003…,则无理数的个数是( )A、1 B、2 C、3 D、46. 下列在数轴上所表示的解集中,不包括 的是( )A、
A、44° B、56° C、45° D、34°5. 已知一组数据 ,π, ,0.0456, ,1.010010003…,则无理数的个数是( )A、1 B、2 C、3 D、46. 下列在数轴上所表示的解集中,不包括 的是( )A、 B、
B、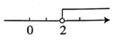 C、
C、 D、
D、 7. 如图3所示,AB∥CD,若∠1=144°,则∠2的度数是( )
7. 如图3所示,AB∥CD,若∠1=144°,则∠2的度数是( )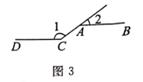 A、30° B、32° C、34° D、36°8. 如图4,数轴上点A与点B表示的数互为相反数若点A表示的数是- ,用圆规在数轴上确定一点C,则与点C对应的实数是( )
A、30° B、32° C、34° D、36°8. 如图4,数轴上点A与点B表示的数互为相反数若点A表示的数是- ,用圆规在数轴上确定一点C,则与点C对应的实数是( )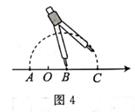 A、 B、2 C、3 D、49. 已知a,b满足方程组 ,则3a+b的值是( )A、-8 B、8 C、4 D、-410. 如图5,点A(2,-1),B(5,3),经过点A的直线l∥y轴,点C为直线L上一点,则当线段BC的长度最小时点C的坐标为( )
A、 B、2 C、3 D、49. 已知a,b满足方程组 ,则3a+b的值是( )A、-8 B、8 C、4 D、-410. 如图5,点A(2,-1),B(5,3),经过点A的直线l∥y轴,点C为直线L上一点,则当线段BC的长度最小时点C的坐标为( )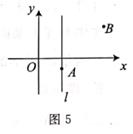 A、(-1,3) B、(1,2) C、(3,2) D、(2,3)11. 如图6,平移折线AEB,得到折线CFD,则平移过程中扫过的面积是( )
A、(-1,3) B、(1,2) C、(3,2) D、(2,3)11. 如图6,平移折线AEB,得到折线CFD,则平移过程中扫过的面积是( )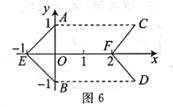 A、4 B、5 C、6 D、712. 下面四种沿AB折叠的方法中,能判定纸带两条边线a,b互相平行的是( )
A、4 B、5 C、6 D、712. 下面四种沿AB折叠的方法中,能判定纸带两条边线a,b互相平行的是( )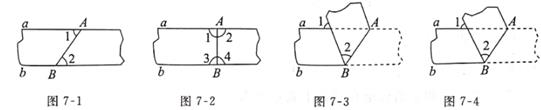
①如图7-1,展开后测得∠1=∠2;②如图7-2,展开后测得∠1=∠2,∠3=∠4;
③如图7-3,测得∠1=70°,∠2=55°;④如图7-4,测得∠1=∠2
A、①③ B、①②③ C、①④ D、①②③④13. 圆柱形水杯和杯中水面的高度如图8-1,放入3个同样的小玻璃球后水面高度如图8-2.若使水杯中有水溢出,则至少需放入小球( )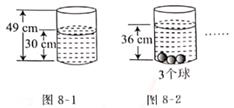 A、9个 B、10个 C、12个 D、16个14. 如图9,直线l1∥l2 , 把一个正方形按如图所示的位置摆放,已知∠1=50°,则∠2的度数为( )
A、9个 B、10个 C、12个 D、16个14. 如图9,直线l1∥l2 , 把一个正方形按如图所示的位置摆放,已知∠1=50°,则∠2的度数为( )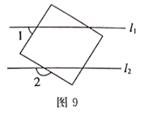 A、120° B、130° C、140 D、150°
A、120° B、130° C、140 D、150°二、填空题(本大题共4个小题,每小题4分,共16分)
-
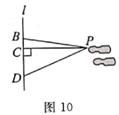
15. 命题“垂直于同一条直线的两条直线平行”的条件是 。16. 计算: = 。17. 在体育课上某同学立定跳远的情况如图10所示,直线l表示起跳线在测量该同学的实际立定跳远成绩时,应测量图中线段 的长,理由是 。
 18. 已知点A(1,0),B(2,2),点C在坐标轴上,且三角形ABC的面积为2,则满足条件的点C的坐标是 。
18. 已知点A(1,0),B(2,2),点C在坐标轴上,且三角形ABC的面积为2,则满足条件的点C的坐标是 。三、解答题(本大题共7个小题共62分)
-
19. 解不等式组 ,请结合题意填空,完成本题的解答。(1)、解不等式①,得;(2)、解不等式②,得 ;(3)、把不等式①和②的解集在数轴上表示出来
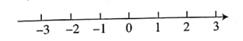 (4)、原不等式组的解集为 。20. 已知:如图11,DG⊥BC,AC⊥BC, ∠1=∠2,试说明:EF∥CD,将过程补充完整。
(4)、原不等式组的解集为 。20. 已知:如图11,DG⊥BC,AC⊥BC, ∠1=∠2,试说明:EF∥CD,将过程补充完整。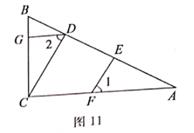
解:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°()
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1= (等量代换)
∴EF∥CD()
21. 对于解方程组 大林同学是这样做的:解:由②,得t=2s+5,③
把③代入①,得45+3(2s+5)=5,
解得s=-1
把s=-1代入②,得t=3
这个方程组的解为
(1)、大林同学解这个方程组的过程中使用了消元法,目的是把二元一次方程转化为;(2)、请你用另一种方法,解这个方程组22. 如图12,在四边形ABCD中,AD∥BC,E为AB边上一点,∠BCE=15°,EF∥AD交DC于点F。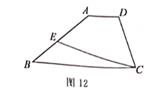 (1)、依题意补全图形,求∠FEC的度数;(2)、若∠A=140°,求∠AEC的度数。23. 某校为了了解学生“最喜欢的运动项目”的情况,设置了五项“单选题”问卷(必选且只选项),随机抽取了部分学生进行问卷调查,并将调在结果制成不完整统计表和统计图(如图13)
(1)、依题意补全图形,求∠FEC的度数;(2)、若∠A=140°,求∠AEC的度数。23. 某校为了了解学生“最喜欢的运动项目”的情况,设置了五项“单选题”问卷(必选且只选项),随机抽取了部分学生进行问卷调查,并将调在结果制成不完整统计表和统计图(如图13)最喜欢的运动项目的人数调查统计表
最喜的项目
篮球
足球
羽毛球
乒乓球
跑步
人数
12
16
10
m
n
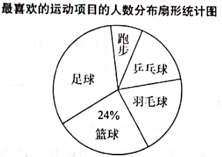
根据以上信息,解决下列问题
(1)、这次调查的样本容量是 , m+n=;(2)、扇形统计图中“羽毛球”对应的扇形的圆心角为;(3)、已知样本中最喜欢乒乓球的人数比最喜欢跑步的人数多4人,且该校有1700名学生,估计该校最喜欢乒乓球的学生人数.24. 某水果店新进a斤樱桃,成本价为每斤30元,为方便销售、减少损耗,将樱桃分装成甲、乙两种礼品箱.设分装甲种礼品箱x箱,乙种礼品箱y箱.每箱数量(斤)
每箱售价(元)
甲种礼品箱
4
240
乙种礼品箱
6
300
(1)、先分装120斤(a>120)樱桃用含x的代数式表示y为;
(2)、若分装好的甲、乙两种礼品箱全部售出,且总利润不少于3000元,则甲种礼品箱的数量至少是多少箱?(3)、若这a斤樱桃全部装箱售出,且平均每斤获得24元的利润,水果店只有70个空箱,求a的最大值。25. 已知 是关于x的二元一次方程kx-y+3=0的一个解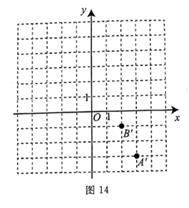 (1)、k= ,用含x的式子表示y为;(2)、完成下表:
(1)、k= ,用含x的式子表示y为;(2)、完成下表:X
-3
-2
y
3
5
(3)、以表中x,y的对应值(从左至右)为点AB,C,D的坐标在图14中描出这些点并按点AB和点A’,B‘的变换关系,写出点D的对应点D‘的坐标;(4)、把点C向右平移4个单位长度到达点P,再把点B向上平移1个单位长度到达点Q,画出△PQC,求△PQC的面积。