2017年高考文数真题试卷（天津卷）

试卷更新日期：2017-06-12 类型：高考真卷

进入出卷网下载

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 设集合A={1，2，6}，B={2，4}，C={1，2，3，4}，则（A∪B）∩C=（　　）

A、{2} B、{1，2，4} C、{1，2，4，6} D、{1，2，3，4，6}

查看试题解析
2. 设x∈R，则“2﹣x≥0”是“|x﹣1|≤1”的（　　）

A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 有5支彩笔（除颜色外无差别），颜色分别为红、黄、蓝、绿、紫．从这5支彩笔中任取2支不同颜色的彩笔，则取出的2支彩笔中含有红色彩笔的概率为（　　）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
4.
阅读如图的程序框图，运行相应的程序，若输入N的值为19，则输出N的值为（　　）

A、0 B、1 C、2 D、3

查看试题解析
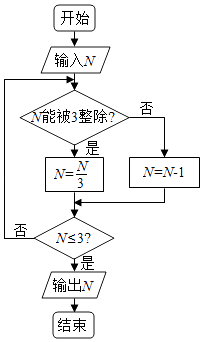5. 已知双曲线 $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的右焦点为F，点A在双曲线的渐近线上，△OAF是边长为2的等边三角形（O为原点），则双曲线的方程为（　　）

A、 $\frac{x^{2}}{4} - \frac{y^{2}}{12} = 1$ B、 $\frac{x^{2}}{12} - \frac{y^{2}}{4} = 1$ C、 $\frac{x^{2}}{3} - y^{2} = 1$ D、 $x^{2} - \frac{y^{2}}{3} = 1$

查看试题解析
6. 已知奇函数f（x）在R上是增函数．若a=﹣f（ $l o g_{2} \frac{1}{5}$ ），b=f（log₂4.1），c=f（2^0.8），则a，b，c的大小关系为（　　）

A、a＜b＜c B、b＜a＜c C、c＜b＜a D、c＜a＜b

查看试题解析
7. 设函数f（x）=2sin（ωx+φ），x∈R，其中ω＞0，|φ|＜π．若f（ $\frac{5 π}{8}$ ）=2，f（ $\frac{11 π}{8}$ ）=0，且f（x）的最小正周期大于2π，则（　　）

A、ω= $\frac{2}{3}$ ，φ= $\frac{π}{12}$ B、ω= $\frac{2}{3}$ ，φ=﹣ $\frac{11 π}{12}$ C、ω= $\frac{1}{3}$ ，φ=﹣ $\frac{11 π}{24}$ D、ω= $\frac{1}{3}$ ，φ= $\frac{7 π}{24}$

查看试题解析
8. 已知函数f（x）= ${\begin{matrix} | x | + 2 ， x < 1 \\ x + \frac{2}{x} ， x \geq 1. \end{matrix}$ ，设a∈R，若关于x的不等式f（x）≥| $\frac{x}{2}$ +a|在R上恒成立，则a的取值范围是（　　）

A、[﹣2，2] B、 $[- 2 \sqrt{3} ， 2]$ C、 $[- 2 ， 2 \sqrt{3}]$ D、 $[- 2 \sqrt{3} ， 2 \sqrt{3}]$

查看试题解析

二、填空题：本大题共6小题，每小题5分，共30分.

9. 已知a∈R，i为虚数单位，若 $\frac{a - i}{2 + i}$ 为实数，则a的值为．

查看试题解析
10. 已知a∈R，设函数f（x）=ax﹣lnx的图象在点（1，f（1））处的切线为l，则l在y轴上的截距为．

查看试题解析
11. 已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为．

查看试题解析
12. 设抛物线y²=4x的焦点为F，准线为l．已知点C在l上，以C为圆心的圆与y轴的正半轴相切于点A．若∠FAC=120°，则圆的方
程为．

查看试题解析
13. 若a，b∈R，ab＞0，则 $\frac{a^{4} + 4 b^{4} + 1}{a b}$ 的最小值为．

查看试题解析
14. 在△ABC中，∠A=60°，AB=3，AC=2．若 $\vec{B D}$ =2 $\vec{D C}$ ， $\vec{A E}$ =λ $\vec{A C}$ ﹣ $\vec{A B}$ （λ∈R），且 $\vec{A D} \cdot \vec{A E}$ =﹣4，则λ的值为．

查看试题解析

三、解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．

15. 在△ABC中，内角A，B，C所对的边分别为a，b，c．已知asinA=4bsinB，ac= $\sqrt{5}$ （a²﹣b²﹣c²）．（13分）

（Ⅰ）求cosA的值；
（Ⅱ）求sin（2B﹣A）的值．

查看试题解析
16. 电视台播放甲、乙两套连续剧，每次播放连续剧时，需要播放广告．已知每次播放甲、乙两套连续剧时，连续剧播放时长、广告播放时长、收视人次如下表所示：

连续剧播放时长（分钟）
广告播放时长（分钟）
收视人次（万）
甲
70
5
60
乙
60
5
25
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟，广告的总播放时间不少于30分钟，且甲连续剧播放的次数不多于乙连续剧播放次数的2倍．分别用x，y表示每周计划播出的甲、乙两套连续剧的次数．（13分）

（I）用x，y列出满足题目条件的数学关系式，并画出相应的平面区域；
（II）问电视台每周播出甲、乙两套连续剧各多少次，才能使总收视人次最多？

查看试题解析
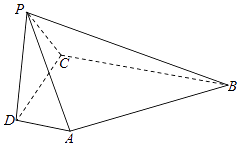
17. 如图，在四棱锥P﹣ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2．（13分）
（I）求异面直线AP与BC所成角的余弦值；
（II）求证：PD⊥平面PBC；
（II）求直线AB与平面PBC所成角的正弦值．

查看试题解析
18. 已知{a_n}为等差数列，前n项和为S_n（n∈N^*），{b_n}是首项为2的等比数列，且公比大于0，b₂+b₃=12，b₃=a₄﹣2a₁ ， S₁₁=11b₄ ．（13分）

（Ⅰ）求{a_n}和{b_n}的通项公式；
（Ⅱ）求数列{a_2nb_n}的前n项和（n∈N^*）．

查看试题解析
19. 设a，b∈R，|a|≤1．已知函数f（x）=x³﹣6x²﹣3a（a﹣4）x+b，g（x）=e^xf（x）．（14分）

（Ⅰ）求f（x）的单调区间；
（Ⅱ）已知函数y=g（x）和y=e^x的图象在公共点（x₀ ， y₀）处有相同的切线，
（i）求证：f（x）在x=x₀处的导数等于0；
（ii）若关于x的不等式g（x）≤e^x在区间[x₀﹣1，x₀+1]上恒成立，求b的取值范围．

查看试题解析
20. 已知椭圆 $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左焦点为F（﹣c，0），右顶点为A，点E的坐标为（0，c），△EFA的面积为 $\frac{b^{2}}{2}$ ．（14分）

（I）求椭圆的离心率；
（II）设点Q在线段AE上，|FQ|= $\frac{3}{2}$ c，延长线段FQ与椭圆交于点P，点M，N在x轴上，PM∥QN，且直线PM与直线QN间的距离为c，四边形PQNM的面积为3c．
（i）求直线FP的斜率；
（ii）求椭圆的方程．

查看试题解析

	连续剧播放时长（分钟）	广告播放时长（分钟）	收视人次（万）
甲	70	5	60
乙	60	5	25