浙江省温州市五校2019届数学中考模拟试卷（3月）

试卷更新日期：2019-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 在－2，0，1， $\sqrt{2}$ 这四个数中，最小的数是（）

A、－2 B、0 C、1 D、 $\sqrt{2}$

查看试题解析
2. PM2.5 是指大气中直径小于或等于 2.5 微米的颗粒物，2.5 微米等于 0.000 002 5 米，把0.0000025 用科学记数法表示为（）

A、2.5×10 ^-6 B、0.25×10 ^-5 C、2.5×10 ⁶ D、25×10 ^-7

查看试题解析
3. “瓦当”是中国古建筑中覆盖檐头筒瓦前端的遮挡，主要有防水、排水、保护木制飞檐和美化屋面轮廓的作用.下面“瓦当”图案中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、x＋x²＝x³ B、2x－3x＝－x C、(x²)³＝x⁵ D、x⁶÷x³＝x²

查看试题解析
5. 某班 6 个合作小组的人数分别是：4，6，4，5，7，8，现第 4 小组调出 1 人去第 2 小组，则调动后各组人数分别为：4，7，4，4，7，8，下列关于调配后的数据说法正确的是（）

A、平均数变小 B、平均数变大 C、方差不变 D、方差变大

查看试题解析
6. 如图，AB 是⊙O 的直径，CD 是⊙O 的弦，若∠ADC=54°，则∠CAB 的度数是（）

A、52° B、36° C、27° D、26°

查看试题解析
7. 图1是一个地铁站入口的双翼闸机.如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°.当双翼收起时，可以通过闸机的物体的最大宽度为（）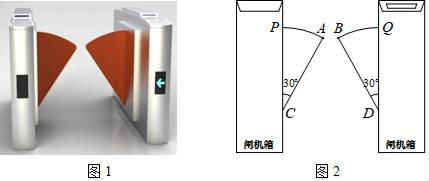

A、(54 $\sqrt{3}$ +10) cm B、(54 $\sqrt{2}$ +10) cm C、64 cm D、54cm

查看试题解析
8. 已知二次函数 y = x²- 4x + n (n 是常数)，若对于抛物线上任意两点 A (x₁ ， y₁ ) ，B (x₂ ， y₂ ) 均有 y₁＞y₂ ，则 x₁ ， x₂ 应满足的关系式是（）

A、x₁ - 2＞x₂- 2 B、x₁ - 2＜x₂ - 2 C、| x₁ - 2|＞|x₂ - 2| D、| x₁ - 2 | ＜|x₂ - 2 |

查看试题解析
9. 如图，矩形 OABC 的顶点 O 在坐标原点，顶点 A，C 分别在 x，y 轴的正半轴上，顶点 B 在反比例函数 y = $\frac{k}{x}$ （k 为常数，k＞0，x＞0）的图象上，将矩形 OABC 绕点 B 逆时针方向旋转 90°得到矩形 BC‘O’A‘，点 O 的对应点O'恰好落在此反比例函数图象上.延长 A’O‘，交 x轴于点 D，若四边形C’ADO‘ 的面积为 2，则 k 的值为（）

A、 $\sqrt{5}$ +1 B、 $\sqrt{5}$ -1 C、2 $\sqrt{5}$ +2 D、2 $\sqrt{5}$ -2

查看试题解析

二、填空题

10. 因式分解：a²﹣2a= ．

查看试题解析
11. 一个扇形的圆心角为 120°，半径为 2，则这个扇形的弧长为.

查看试题解析
12. 小亮做抛掷硬币的实验时，他抛掷一枚均匀的硬币 3 次，均正面朝上.则小亮第 4 次抛掷这枚硬币，正面朝上的概率为.

查看试题解析
13. 某工厂现在平均每天比原计划多生产50台机器，现在生产800台所需时间与原计划生产600台机器所需时间相同.设原计划平均每天生产x台机器，根据题意可列出方程.

查看试题解析
14. 如图，△ABC 中，∠C=90°，CA=CB，D 为 AC 上的一点，AD=3CD，AE⊥AB 交 BD 延长线于 E，记△EAD，△DBC 的面积分别为 S₁ ， S₂ ，则 S₁：S₂=.

查看试题解析
15. 如图 1 是台湾某品牌手工蛋卷的外包装盒，其截面图如图 2 所示，盒子上方是一段圆弧（弧 MN ）.D，E 为手提带的固定点， DE 与弧MN 所在的圆相切，DE=2.手提带自然下垂时，最低点为C，且呈抛物线形，抛物线与弧MN 交于点 F，G.若△CDE 是等腰直角三角形，且点 C，F 到盒子底部 AB 的距离分别为 1， $\frac{9}{4}$ ，则弧MN 所在的圆的半径为.

查看试题解析

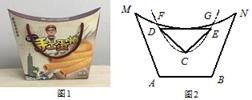
三、解答题

16.

(1)、计算：2cos30°+ 3^-¹ + $\sqrt{12}$

(2)、化简：(a+b)( a－b)－a (a+b)

查看试题解析

17. 某次模拟考试后，抽取 m 名学生的数学成绩进行整理分组，形成如下表格（x 代表成绩），并绘制出扇形统计图和频数分布直方图（横坐标表示成绩，单位：分）.

A 组	140＜x≤150
B 组	130＜x≤140
C 组	120＜x≤130
D 组	110＜x≤120
E 组	100＜x≤110

(1)、m 的值为多少，扇形统计图中 D 组对应的圆心角是多少度.

(2)、请补全条形统计图，并标注出相应的人数.

(3)、若此次考试数学成绩 130 分以上的为优秀，参加此次模拟考的学生总数为 2000，请估算此次考试数学成绩优秀的学生人数.

查看试题解析

18. 如图，点 A，B，C，D 依次在同一条直线上，点 E，F 分别在直线 AD 的两侧，已知 BE//CF，∠A=∠D，AE=DF.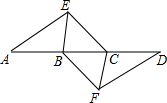

(1)、求证：四边形 BFCE 是平行四边形.

(2)、若 AD=10，EC=3，∠EBD=60°，当四边形 BFCE是菱形时，求 AB 的长.

查看试题解析
19. 如图，在方格纸中，点A，B，P，Q都在格点上.请按要求画出以AB为边的格点四边形.

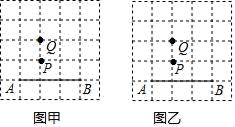(1)、在图甲中画出一个▱ABCD，使得点P为▱ABCD的对称中心；

(2)、在图乙中画出一个▱ABCD，使得点P，Q都在▱ABCD的对角线上.

查看试题解析
20. 如图是一个倾斜角为a 的斜坡，将一个小球从斜坡的坡脚 O 点处抛出，落在 A点处，小球的运动路线可以用抛物线 $y = - \frac{1}{2} {(x - m)}^{2} + \frac{9}{2}$ 来刻画，已知 tan a = $\frac{1}{2}$ .

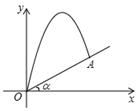(1)、求抛物线表达式及点 A 的坐标.

(2)、求小球在运动过程中离斜坡坡面 OA 的最大距离.

查看试题解析
21. 如图，AB 是⊙O 的弦，半径OE⊥ AB ，P 为 AB 的延长线上一点，PC 与⊙O相切于点 C，连结 CE，交 AB 于点 F，连结 OC.

(1)、求证：PC=PF.

(2)、连接 BE，若∠CEB=30°，半径为 8，tan P = $\frac{4}{3}$ ，求 FB 的长.

查看试题解析
22. 某甜品店用 A，B 两种原料制作成甲、乙两款甜品进行销售，制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品 x 份，乙款甜品 y 份，共用去A 原料 2000 克.

(1)、求 y 关于 x 的函数表达式.

(2)、已知每份甲甜品的利润为 a 元(a 正整数)，每份乙甜品的利润为 2 元. 假设两款甜品均能全部卖出.
①当 a=3 时，若获得总利润不少于 220 元，则至少要用去 B 原料多少克？

②现有 B 原料 3100 克，要使获利为 450 元且尽量不浪费原材料，甲甜品的每份利润应定为多元？

查看试题解析
23. 如图，在平面直角坐标系中，A(0，4)，B(3，4)，P 为线段 OA 上一动点，过 O，P，B 三点的圆交 x 轴正半轴于点 C，连结 AB， PC，BC，设 OP=m.

(1)、求证：当 P 与 A 重合时，四边形 POCB 是矩形.

(2)、连结 PB，求 tan∠BPC 的值.

(3)、记该圆的圆心为 M，连结 OM，BM，当四边形 POMB 中有一组对边平行时，求所有满足条件的 m 的值.

(4)、作点 O 关于 PC 的对称点O' ，在点 P 的整个运动过程中，当点O' 落在△APB 的内部 (含边界)时，请写出 m 的取值范围.

查看试题解析