浙江省杭州市下城区2019届数学中考一模试卷

试卷更新日期：2019-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算（﹣3）²的结果是（）

A、﹣6 B、6 C、﹣9 D、9

查看试题解析
2. 因式分解：a²﹣4＝（）

A、（a﹣2）（a+2） B、（2﹣a）（2÷a） C、（a﹣2）² D、（a﹣2）（﹣a+2）

查看试题解析
3. 在等腰三角形ABC中，AB＝4，BC＝2，则△ABC的周长为（）

A、8 B、10 C、8或10 D、6或8

查看试题解析
4. 若实数k满足3＜k＜4，则k可能的值是（）

A、2 $\sqrt{2}$ B、2 $\sqrt{3}$ C、 $\frac{\sqrt{15}}{2}$ D、|1﹣π|

查看试题解析
5. 下列计算正确的是（）

A、2（x﹣1）﹣（x﹣1）＝x﹣3 B、 $\frac{1}{a} + \frac{2}{a} = \frac{3}{2 a}$ C、 $\frac{y}{x - y} - \frac{x}{x - y} = - 1$ D、（x+1）÷y× $\frac{1}{y}$ ＝x+1

查看试题解析
6. 在△ABC中，D是BC边上的点（不与B，C重合），连接AD，下列表述错误的是（）

A、若AD是BC边的中线，则BC＝2CD B、若AD是BC边的高线，则AD＜AC C、岩AD是∠BAC的平分线，则△ABD与△ACD的面积相等 D、若AD是∠BAC的平分线又是BC边的中线，则AD为BC边的高线

查看试题解析
7. 小明用100元钱去购买笔记本和钢笔共30件，已知每本笔记本3元，每支钢笔5元，求小明最多能买几支钢笔.设小明买了x支钢笔，依题意可列不等式为（）

A、3x+5（30﹣x）≤100 B、3（30﹣x）+5≤100 C、5（30﹣x）≤100+3x D、5x≤100﹣3（30+x）

查看试题解析
8. 如图，在△ABC中，以边BC为直径做半圆，交AB于点D，交AC于点E，连接DE，若 $\overset{⌢}{D E}$ ＝2 $\overset{⌢}{B D}$ ＝2 $\overset{⌢}{C E}$ ，则下外说法正确的是（）

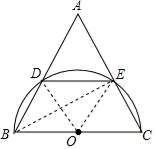A、AB＝ $\sqrt{3}$ AE B、AB＝2AE C、3∠A＝2∠C D、5∠A＝3∠C

查看试题解析
9. 如图，直线l₁∥l₂∥l₃ ， △ABC的三个顶点分別落在l₁∥l₂∥l₃上，AC交l₂与点D.设l₁与l₂的距离为h₁ ， l₂与l₃的距离为h₂.若AB＝BC，h₁：h₂＝1：2，则下列说法正确的是（）

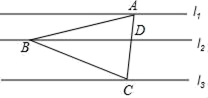A、S_△_ABD：S_△_ABC＝2：3 B、S_△_ABD：S_△_ABC＝1：2 C、sin∠ABD：sin∠DBC＝2：3 D、sin∠ABD：sin∠DBC＝1：2

查看试题解析
10. 已知二次函数y＝﹣（x﹣k+2）（x+k）+m，其中k，m为常数.下列说法正确的是（）

A、若k≠1，m≠0，则二次函数y的最大值小于0 B、若k＜1，m＞0，则二次函数y的最大值大于0 C、若k＝1，m≠0，则二次函数y的最大值小于0 D、若k＞1，m＜0，则二次函数y的最大值大于0

查看试题解析

二、填空题

11. 四张卡片上分别写着﹣2，1，0，﹣1.若从中随机抽出一张，则此卡片上的数为负数的概率是.

查看试题解析
12. 如图，过圆外一点P作⊙O的切线PC，切点为B，连结OP交圆于点A.若AP＝0A＝1，则该切线长为.

查看试题解析
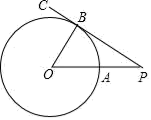13. 两组数据：3，a，8，5与a，6，b的平均数都是6，若将这两组数据合并为一组，则这组新数据的中位数为.

查看试题解析
14. 已知实数x满足 $\sqrt{x - 2}$ •|x+1|≤0，则x的值为.

查看试题解析
15. 如图，在直角△ABC中，∠ACB＝90°，AC＝3，BC＝4，且点D，E分別在BC，AB上，连结AD和CE交于点H.若 $\frac{B D}{C D}$ ＝2， $\frac{A H}{D H}$ ＝1，则BE的长为.

查看试题解析
16. 已知实数x，y，a满足x+3y+a＝4，x﹣y﹣3a＝0.若﹣1≤a≤1，则2x+y的取值范围是.

查看试题解析

三、解答题

17. 某研究小组用随机抽样的方法，在本校初三年级开展了“你最喜欢的电视节目”调查，并将得到的数据整理成了以下统计图（不完整）.

(1)、此次研究小组共调查了多少名学生？

(2)、若该学校初三年级共有300名学生，请你估计其中最喜欢“体育节目”的有多少.

查看试题解析
18. 在平面直角坐标系中，一次函数y＝kx+b的图象过点（1，2），且b＝k+4.

(1)、当x＝3时，求y的值.

(2)、若点A（a﹣1，2a+6）在一次函数图象上，试求a的值.

查看试题解析
19. 如图，在△ABC中，D为AB上的一点，过点D作DE∥AC，DF∥BC，分别交BC，AC于点E，F.

(1)、求证：△ADF∽△DBE.

(2)、若BE：CE＝2：3，求AF：DE的值.

查看试题解析
20. 如图，某农家拟用已有的长为8m的墙或墙的一部分为一边，其它三边用篱笆围成一个面积为12m²的矩形园子.设园子中平行于墙面的篱笆长为ym（其中y≥4），另两边的篱笆长分别为xm.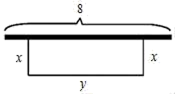

(1)、求y关于x的函数表达式，并求x的取值范围.

(2)、若仅用现有的11m长的篱笆，且恰好用完，请你帮助设计围制方案.

查看试题解析
21. 在△ABC中，BD⊥AC于点D，P为BD上的点，∠ACP＝45°，AP＝BC.

(1)、求证：AD＝BD

(2)、若∠CPA＝120°，BC＝2，求PB的长.

查看试题解析
22. 在平面直角坐标系中，二次函数图象的表达式为y＝ax²+（a+1）x，其中a≠0.

(1)、若此函数图象过点（1，﹣3），求这个二次函数的表达式.

(2)、若（x₁ ， y₁）（x₂ ， y₂）为此二次函数图象上两个不同点
①若x₁+x₂＝2，则y₁＝y₂ ，试求a的值.

②当x₁＞x₂≥﹣2，对任意的x₁ ， x₂都有y₁＞y₂ ，试求a的取值范围.

查看试题解析
23. 在菱形ABCD中，E，F分别为BC，CD上点，且CE＝CF，连结AE，AF，EF.记△CEF的面积为m，△AEF的面积为n.

(1)、求证：△ABE≌△ADF.

(2)、若AE⊥BC，CF：AE＝2：3，求sinD.

(3)、设BE：EC＝a，m＝3﹣a，试说明当a取何值时n的值最大，并求出n的最大值.

查看试题解析