浙江省富阳市2019届数学中考模拟试卷(3月)
试卷更新日期:2019-07-23 类型:中考模拟
一、单选题
-
1. 下列数中最大的是( )A、-3 B、0 C、π D、2. 银河系中大约有恒星160 000 000 000颗,数据160 000 000 000用科学记数法表示为( )A、0.16×1012 B、1.6×1011 C、16×1010 D、160×1093. 用100元钱在网上书店恰好可购买m本书,但是每本书需另加邮寄费6角,购买n本书共需费用y元,则可列出关系式( )A、 B、 C、 D、4. 布袋中装着只有颜色不同的红、黄、黑小球各一个,从中任意摸出一个球,记下颜色后放回搅匀,再摸出一个球,则摸出一个红球,一个黑球的概率是( )A、 B、 C、 D、5. 一个几何体的三视图如图所示,该几何体是( )
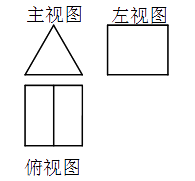 A、直三棱柱 B、长方体 C、圆锥 D、立方体6. 如图,△ABC内接于⊙O,若∠A=α度,则∠OBC的度数为( )
A、直三棱柱 B、长方体 C、圆锥 D、立方体6. 如图,△ABC内接于⊙O,若∠A=α度,则∠OBC的度数为( )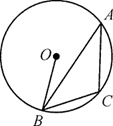 A、α B、90-α C、90+α D、90+2α7. 如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )
A、α B、90-α C、90+α D、90+2α7. 如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )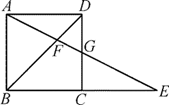 A、6 B、8 C、10 D、128. 已知点A(-1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可能是( )A、
A、6 B、8 C、10 D、128. 已知点A(-1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可能是( )A、 B、
B、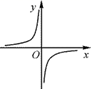 C、
C、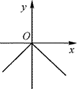 D、
D、 9. 四位同学在研究函数y1=ax2+ax-2a (a是非零常数)时,甲发现该函数图象总经过定点;乙发现若抛物线y1=ax2+ax-2a总不经过点P(x0-3,x02-16),则符合条件的点P有且只有2个;丙发现若直线y2=kx+b与函数y1交于x轴上同一点,则b=-k;丁发现若直线y3=m (m≠0)与抛物线有两个交点(x1 , y1)(x2 , y2),则x1+x2+1=0.已知这四位同学中只有一位发现的结论是错误的,则该同学是( )A、甲 B、乙 C、丙 D、丁10. 如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )
9. 四位同学在研究函数y1=ax2+ax-2a (a是非零常数)时,甲发现该函数图象总经过定点;乙发现若抛物线y1=ax2+ax-2a总不经过点P(x0-3,x02-16),则符合条件的点P有且只有2个;丙发现若直线y2=kx+b与函数y1交于x轴上同一点,则b=-k;丁发现若直线y3=m (m≠0)与抛物线有两个交点(x1 , y1)(x2 , y2),则x1+x2+1=0.已知这四位同学中只有一位发现的结论是错误的,则该同学是( )A、甲 B、乙 C、丙 D、丁10. 如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )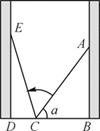 A、0.7米 B、1.5米 C、2.2米 D、2.4米
A、0.7米 B、1.5米 C、2.2米 D、2.4米二、填空题
-
11. = .12. 分解因式4x2-(y-2)2=.13. 圆心角为120º的扇形的面积为12π,则扇形的弧长为.14. 如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠BAC=25°,则∠P=度.
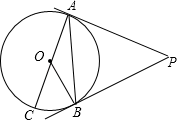 15. 已知关于x的代数式 ,当x=时,代数式的最小值为.16. 已知直线y1=kx+1(k<0)与直线y2=nx(n>0)的交点坐标为( , ),则不等式组nx-3<kx+1<nx的解集为.
15. 已知关于x的代数式 ,当x=时,代数式的最小值为.16. 已知直线y1=kx+1(k<0)与直线y2=nx(n>0)的交点坐标为( , ),则不等式组nx-3<kx+1<nx的解集为.三、解答题
-
17. 我们知道,海拔高度每上升1km,温度下降6℃.某时刻,杭州地面温度为20℃,设高出地面xkm处的温度是y℃.(1)、求y与x的函数关系式.(2)、在同一时刻,有一架飞机飞过杭州上空,若机舱内仪表显示飞机外的温度为-34℃,求这架飞机距离地面的高度.18. 甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.(1)、请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.(2)、若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.19. 如图,在△ABC中,∠ACB=90°,sin A= ,BC=8,D是AB中点,过点B作直线CD的垂线,垂足为点E.
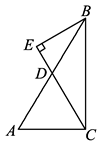 (1)、求线段CD的长;(2)、求cos ∠ABE的值.20. 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
(1)、求线段CD的长;(2)、求cos ∠ABE的值.20. 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.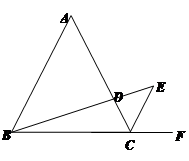 (1)、求证:△ABD∽△CED.(2)、若AB=6,AD=2CD,求BE的长.21. 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.
(1)、求证:△ABD∽△CED.(2)、若AB=6,AD=2CD,求BE的长.21. 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.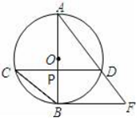 (1)、求证:直线BF是⊙O的切线.(2)、若CD=2 ,OP=1,求线段BF的长.22. 已知关于x的一元二次方程x2-(m+1)x+ (m2+1)=0.(1)、若该方程有实数根,求m的值.(2)、对于函数y1=x2-(m+1)x+ (m2+1),当x>1时,y1随着x的增大而增大.
(1)、求证:直线BF是⊙O的切线.(2)、若CD=2 ,OP=1,求线段BF的长.22. 已知关于x的一元二次方程x2-(m+1)x+ (m2+1)=0.(1)、若该方程有实数根,求m的值.(2)、对于函数y1=x2-(m+1)x+ (m2+1),当x>1时,y1随着x的增大而增大.①求m的范围.
②若函数y2=2x+n与函数 交于y轴上同一点,求n的最小值.
23. △ABC和△ADE是有公共顶点的三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.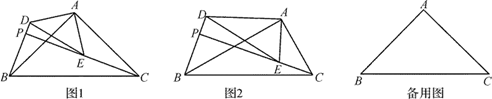 (1)、①如图1,∠ADE=∠ABC=45°,求证:∠ABD=∠ACE.
(1)、①如图1,∠ADE=∠ABC=45°,求证:∠ABD=∠ACE.②如图2,∠ADE=∠ABC=30°,①中的结论是否成立?请说明理由.
(2)、在(1) ①的条件下,AB=6,AD=4,若把△ADE绕点A旋转,当∠EAC=90°时,画图并求PB的长度.