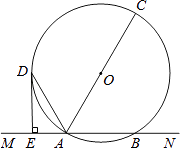云南省昆明市2019届数学中考模拟试卷(5月)
试卷更新日期:2019-07-23 类型:中考模拟
一、单选题
-
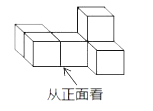
1. 昆明市有关负责人表示,预计 年昆明市的地铁修建资金将达到 亿元,将 亿用科学记数法表示为( )A、 B、 C、 D、2. 下图是由 个大小相同的小正方体组成的几何体,它的左视图是( )
 A、
A、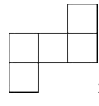 B、
B、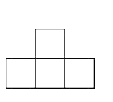 C、
C、 D、
D、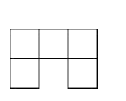 3. 小明记录了昆明市 年 月份某一周每天的最高气温,如表:
3. 小明记录了昆明市 年 月份某一周每天的最高气温,如表:日期
最高气温
那么这周每天的最高气温 的众数和中位数分别是( )
A、 , B、 , C、 , D、 ,4. 下列运算正确的是( )A、 B、 C、 D、5. 如图, , 交 于点 , , ,则 的度数为( ) A、 B、 C、 D、6. 如图,在菱形ABCD中,∠BAC=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC,AD于点F、G,连接OG,则下列结论中一定成立的是( ).
A、 B、 C、 D、6. 如图,在菱形ABCD中,∠BAC=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC,AD于点F、G,连接OG,则下列结论中一定成立的是( ).①OG= AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.
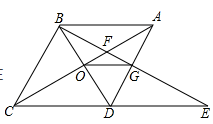 A、①③④ B、①④ C、①②③ D、②③④7. 刘主任乘公共汽车从昆明到相距 千米的晋宁区办事,然后乘出租车返回,出租车的平均速度比公共汽车快 千米/时,回来时路上所花时间比去时节省了 小时,设公共汽车的平均速度为 千米 时,则下面列出的方程中正确的是( )A、 B、 C、 D、8. 如图,正方形 的边长为 ,点 的坐标为 ,点 在 轴上,若反比例函数 的图象过点 ,则该反比例函数的表达式为( )
A、①③④ B、①④ C、①②③ D、②③④7. 刘主任乘公共汽车从昆明到相距 千米的晋宁区办事,然后乘出租车返回,出租车的平均速度比公共汽车快 千米/时,回来时路上所花时间比去时节省了 小时,设公共汽车的平均速度为 千米 时,则下面列出的方程中正确的是( )A、 B、 C、 D、8. 如图,正方形 的边长为 ,点 的坐标为 ,点 在 轴上,若反比例函数 的图象过点 ,则该反比例函数的表达式为( )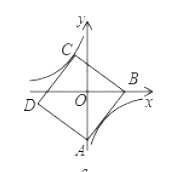 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如果 的相反数是 ,那么 的值是.10. 要使 有意义,则 的取值范围是.11. 如果 ,那么代数式 的值是.12. 如图, 中, , , 平分 交 于点 ,点 为 的中点,连接 ,则 的周长为.
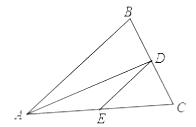 13. 关于 的一元二次方程 有两个实数根,则 的取值范围是.14. 如图,点 是圆形纸片的圆心,将这个圆形纸片按下列要求折叠,使弧 和弧 都经过圆心 ,已知 的半径为 ,则阴影部分的面积是.
13. 关于 的一元二次方程 有两个实数根,则 的取值范围是.14. 如图,点 是圆形纸片的圆心,将这个圆形纸片按下列要求折叠,使弧 和弧 都经过圆心 ,已知 的半径为 ,则阴影部分的面积是.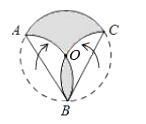
三、解答题
-
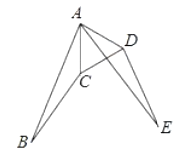
15. 计算: .16. 如图,已知 是等边三角形, , .求证: .
 17. 如图,方格中每个小正方形的边长都是单位 , 在平面直角坐标系中的位置如图.
17. 如图,方格中每个小正方形的边长都是单位 , 在平面直角坐标系中的位置如图.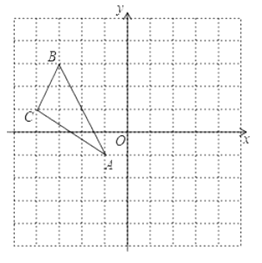 (1)、①画出 关于 轴对称的 ;
(1)、①画出 关于 轴对称的 ;②画出 绕点 按逆时针方向旋转 后的 ;
(2)、直接写出过点 、 两点的直线的函数解析式.18. 昆明市某校学生会干部对校学生会倡导的“牵手滇西”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1:5.组别
捐款额x/元
人数
A
1≤x<10
a
B
10≤x<20
100
C
20≤x<30
D
30≤x<40
E
40≤x<50
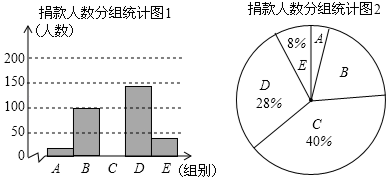
请结合以上信息解答下列问题.
(1)、a= , 本次调查样本的容量是;(2)、先求出C组的人数,再补全“捐款人数分组统计图1”;(3)、根据统计情况,估计该校参加捐款的4500名学生有多少人捐款在20至40元之间.19. 已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求: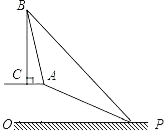 (1)、坡顶A到地面PO的距离;(2)、古塔BC的高度(结果精确到1米).
(1)、坡顶A到地面PO的距离;(2)、古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
20. 昆明市某中学“综合实践活动”棋类社团前两次购买的两种材质的围棋采购如表(近期两种材质的围棋的售价一直不变):塑料围棋
玻璃围棋
总价(元)
第一次(盒)
第二次(盒)
(1)、若该社团计划再采购这两种材质的围棋各 盒,则需要多少元;(2)、若该社团准备购买这两种材质的围棋共 盒,且要求塑料围棋的数量不多于玻璃围棋数量的 倍,请设计出最省钱的购买方案,并说明理由.