云南省昆明市2019届数学中考模拟试卷（4月）

试卷更新日期：2019-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 十九大报告中提到：在未来的三年里，城镇每年需要安排的就业人员数量仍超过15000000人，大多是青年学生．这里15000000，可以用科学记数法记为（）

A、1.5×10⁸ B、15×10⁶ C、1.5×10⁶ D、1.5×10⁷

查看试题解析
2. 下列运算不正确的是（）

A、（x﹣1）²＝x²﹣1 B、2a³+a³＝3a³ C、（﹣a）²•a³＝a⁵ D、（a^﹣²）³＝a^﹣⁶

查看试题解析
3. 如图是由五个相同的小正方体搭成的一个几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 从九年级一班参加跳绳考试的同学中随机抽取10名同学的考试成绩如下：193，184，180，186，180，186，184，186，184，186（单位：厘米）.下列表述不正确的是（）

A、众数是186 B、平均数是185 C、中位数是185 D、极差是13

查看试题解析
5. 如图，在矩形ABCD中，AD＝2，tan∠ABD＝2，点E，F在AD，BC上，则菱形AECF的面积为（）

A、1.25 B、5 C、 $\sqrt{7}$ D、2 $\sqrt{7}$

查看试题解析
6. 如图，将一块三角板叠放在直尺上，若∠2＝68°，则∠1的度数为（）

A、12° B、22° C、34° D、68°

查看试题解析
7. 如图，经过点B（﹣1，0）的直线y＝kx+b与直线y＝﹣2x+2相交于点A（m， $\frac{8}{3}$ ），则不等式﹣2x+2＜kx+b的解集为（）

A、x＜﹣ $\frac{1}{3}$ B、x＞1 C、x＜1 D、x＞﹣ $\frac{1}{3}$

查看试题解析
8. 如图所示，反比例函数y＝ $\frac{k}{x}$ （x＜0）的图象经过矩形OABC的对角线AC的中点M，分别与AB，BC交于点D，E，若矩形OABC的面积为8，则k的值为（）

A、﹣2 $\sqrt{2}$ B、﹣2 $\sqrt{5}$ C、2 D、﹣2

查看试题解析

二、填空题

9. 计算：|﹣ $\sqrt{3}$ |= ．

查看试题解析
10. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
11. 如图，点D、E、F分别是△ABC的边AB、BC、CA的中点，连接DE、EF、FD得△DEF，如果△ABC的周长是48cm，那么△DEF的周长是.

查看试题解析
12. 如图，AB是⊙O的直径，C，D两点在⊙O上，若∠BCD＝40°，则∠ABD的度数为．

查看试题解析
13. 已知：m﹣ $\frac{1}{m}$ ＝5，则m²+ $\frac{1}{m^{2}}$ ＝.

查看试题解析
14. 如图，一束平行太阳光照射到每个内角都相等的五边形上，若∠1＝47°，则∠2＝.

查看试题解析

三、解答题

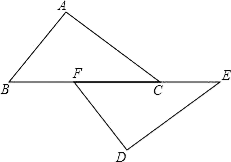
15. 计算： ${(π - 3)}^{0} + {(- 1)}^{2019} + {(- \frac{1}{2})}^{- 2 \times \sqrt[3]{- 8}}$ .

查看试题解析
16. 如图，已知：点B、F、C、E在一条直线上，∠B＝∠E，BF＝CE，AC∥DF.求证：△ABC≌△DEF.

查看试题解析
17. 观察下列各个等式的规律：
第一个等式： $1 + \frac{0}{2} + 1 \times \frac{0}{2} = 1$ ，

第二个等式： $\frac{1}{2} + \frac{1}{3} + \frac{1}{2} \times \frac{1}{3} = 1$

第三个等式： $\frac{1}{3} + \frac{2}{4} + \frac{1}{3} \times \frac{2}{4} = 1$

第四个等式： $\frac{1}{4} + \frac{3}{5} + \frac{1}{4} \times \frac{3}{5} = 1$

…

请用上述等式反映出的规律解决下列问题：

(1)、直接写出第六个等式；

(2)、猜想第n个等式（用n的代数式表示），并证明你猜想的等式是正确的.

查看试题解析
18. 顶点在网格交点的多边形叫做格点多边形，如图，在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.

(1)、在网格中画出△ABC向上平移5个单位，在向左平移4个单位后得到的△A₁B₁C₁；

(2)、在网格中画出△ABC绕点O逆时针旋转90°后得到的△A₂B₂C₂；

(3)、从A到A₂.所划过的痕迹长为多少？

查看试题解析
19. 数学社团小组想利用所学的知识了解某广告牌的高度（图中GH的长），经测量知CD=2m，在B处测得点D的仰角为60°，在A处测得点C的仰角为30°，AB=10m，且A、B、H三点在一条直线上，请根据以上数据计算GH的长（ $\sqrt{3}$ =1.73，要求结果精确得到0.1m）

查看试题解析
20. 某区域为响应“绿水青山就是金山银山”的号召，加强了绿化建设.为了解该区域群众对绿化建设的满意程度，某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查，得到如下不完整统计图.

请结合图中信息，解决下列问题：

(1)、此次调查中接受调查的人数为多少人，其中“非常满意”的人数为多少人；

(2)、兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访，已知这4位群众中有2位来自甲片区，另2位来自乙片区，请用画树状图或列表的方法求出选择的群众来自甲片区的概率.

查看试题解析
21. 为迎接“六一”儿童节，某儿童品牌玩具专卖店购进了A、B两种玩具，其中A类玩具5套B玩具6套，则需950元，A类玩具3套B玩具2套，则需450元

(1)、求A、B两类玩具的进价分别是每个多少元？

(2)、该玩具店购进B类玩具比A类玩具的2倍多4套，且B类玩具最多可购进40套，若玩具店将销售1套A类玩具获利30元，销售1套B类玩具获利20元，且全部售出后所获得利润不少于1200元，问有几种进货方案？如何进货？

查看试题解析
22. 如图，⊙O的半径OA＝4，AB是弦，直线EF经过点B，AC⊥EF于点C，∠BAC＝∠OAB.

(1)、求证：EF是⊙O的切线；

(2)、若AC＝2，求AB的长；

(3)、在（2）的条件下，求图中阴影部分的面积.

查看试题解析
23. 如图，抛物线y＝x²﹣ $\sqrt{2}$ x﹣4与x轴相交于A、B两点（点A在点B的左侧），与y轴交于点C，顶点为 D.

(1)、求出A、B两点的坐标；

(2)、连接AC，点P为第四象限抛物线上的一个动点，P的坐标为P（t，p），四边形ACPB面积为S，求S与t的函数关系式，并求t为何值时，S最大？

(3)、在（2）的基础上，若点M为抛物线上的一个动点，在抛物线对称轴上是否存在这样的点N，使以A、M、P、N为顶点的四边形是平行四边形？如果存在，直接写出满足条件的M，N点的坐标；如果不存在，请说明理由.

查看试题解析