云南省昆明市2019届九年级下学期中考适应性考试数学试卷(三)
试卷更新日期:2019-07-23 类型:期中考试
一、单选题
-
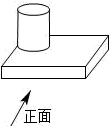
1. 平方根和立方根都是本身的数是( )A、0 B、0和1 C、±1 D、0和±12. 如图,几何体的左视图是( )
 A、
A、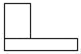 B、
B、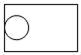 C、
C、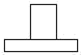 D、
D、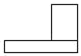 3. 下列计算正确的是( )A、2﹣2=﹣4 B、 =2 C、2a3+3a2=5a5 D、(a5)2=a74. 若一个多边形的内角和比外角和的2倍少180°,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形5. 如图,直线y=﹣x+b与反比例函数y= (k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACO=S△BEO;④S△CEO=15;⑤点D的坐标为(5,0).其中正确的是( )
3. 下列计算正确的是( )A、2﹣2=﹣4 B、 =2 C、2a3+3a2=5a5 D、(a5)2=a74. 若一个多边形的内角和比外角和的2倍少180°,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形5. 如图,直线y=﹣x+b与反比例函数y= (k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACO=S△BEO;④S△CEO=15;⑤点D的坐标为(5,0).其中正确的是( ) A、①②③ B、①②③④ C、②③④⑤ D、①②③⑤6. 如图, 方格纸上的两条对称轴 、 相交于中心点 ,对△ABC分别作下列变换:
A、①②③ B、①②③④ C、②③④⑤ D、①②③⑤6. 如图, 方格纸上的两条对称轴 、 相交于中心点 ,对△ABC分别作下列变换:①先以点 为中心顺时针方向旋转 ,再向右平移 格、向上平移 格;②先以点 为中心作中心对称图形,再以点 的对应点为中心逆时针方向旋转 ;③先以直线 为轴作轴对称图形,再向上平移 格,再以点 的对应点为中心顺时针方向旋转 .其中,能将△ABC变换成△PQR的是( )
 A、①② B、①③ C、②③ D、①②③7. 我市去年有4.7万名考生参加了中考,为了解这些考生的数学成绩,从中抽取了4000名考生的数学成绩进行统计分析,以下说法正确的是( )A、这4000名考生是总体的一个样本 B、这4.7万名考生的数学成绩是总体 C、每位考生是个体 D、抽取的4000名考生是样本容量8. 如图,⊙O与正方形ABCD是两边AB,AD相切,DE与⊙O相切于点E,若正方形ABCD的边长为5,DE=3,则tan∠ODE为( )
A、①② B、①③ C、②③ D、①②③7. 我市去年有4.7万名考生参加了中考,为了解这些考生的数学成绩,从中抽取了4000名考生的数学成绩进行统计分析,以下说法正确的是( )A、这4000名考生是总体的一个样本 B、这4.7万名考生的数学成绩是总体 C、每位考生是个体 D、抽取的4000名考生是样本容量8. 如图,⊙O与正方形ABCD是两边AB,AD相切,DE与⊙O相切于点E,若正方形ABCD的边长为5,DE=3,则tan∠ODE为( )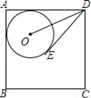 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
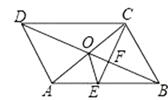
9. 绝对值不大于3的所有整数的积是10. 春节期间,某景区共接待游客约1260000人次,将“1260000”用科学记数法表示为.11. 因式分解:9a3b﹣ab=.12. 如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②S▱ABCD=AC•BC;③OE:AC= :6; ④S▱OEF= S▱ABCD , 成立的是 .
 13. 一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式拼接.若用餐的人数有90人,则这样的餐桌需张.
13. 一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式拼接.若用餐的人数有90人,则这样的餐桌需张. 14. 图 是一个三角形,分别连接这个三角形的中点得到图 ;再分别连接图 中间小三角形三边的中点,得到图 按上面的方法继续下去,第n个图形中有个三角形 用含字母n的代数式表示 .
14. 图 是一个三角形,分别连接这个三角形的中点得到图 ;再分别连接图 中间小三角形三边的中点,得到图 按上面的方法继续下去,第n个图形中有个三角形 用含字母n的代数式表示 .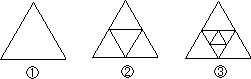
三、解答题
-
15. 解不等式组 ,并把不等式组的解集在数轴上表示出来.
 16. 如图,在平行四边形ABCD中,E、F分别为BC、AD上的点,且∠1=∠2.求证:AF=CE.
16. 如图,在平行四边形ABCD中,E、F分别为BC、AD上的点,且∠1=∠2.求证:AF=CE. 17. “绿水青山就是金山银山”,高新区凌水河治理工程正式启动,若由甲工程队单独完成需10个月;若由甲、乙两工程队合做4个月后,剩下工程由乙工程队再做5个月可以完成。(1)、乙工程队单独完成这项工程需几个月的时间?(2)、已知甲工程队每月施工费用为15万元,比乙工程队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲、乙工程队同时开工,甲工程队做 个月,乙工程队做 个月( 均为整数)分工合作的方式施工,问有哪几种施工方案?18. 某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度,在河的北岸边点A处,测得河的南岸边点B处在其南偏东45°方向,然后向北走20米到达点C处,测得点B在点C的南偏东33°方向,求出这段河的宽度.(结果精确到1米,参考数据:sin33°=0.54,cos33°≈0.84,tan33°=0.65, ≈1.41)
17. “绿水青山就是金山银山”,高新区凌水河治理工程正式启动,若由甲工程队单独完成需10个月;若由甲、乙两工程队合做4个月后,剩下工程由乙工程队再做5个月可以完成。(1)、乙工程队单独完成这项工程需几个月的时间?(2)、已知甲工程队每月施工费用为15万元,比乙工程队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲、乙工程队同时开工,甲工程队做 个月,乙工程队做 个月( 均为整数)分工合作的方式施工,问有哪几种施工方案?18. 某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度,在河的北岸边点A处,测得河的南岸边点B处在其南偏东45°方向,然后向北走20米到达点C处,测得点B在点C的南偏东33°方向,求出这段河的宽度.(结果精确到1米,参考数据:sin33°=0.54,cos33°≈0.84,tan33°=0.65, ≈1.41)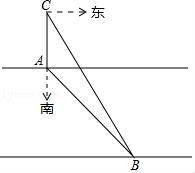 19. 重庆八中将于2017年整体搬迁至渝北空港新城,新校园工程建设正在如火如荼的进行.经工程部管理人员同意,四位同学前往工地进行社会实践活动.如图,A、B、C是三个建筑原材料存放点,点B、C分别位于点A的正北和正东方向,AC=400米.四人分别测得∠C的度数如表:
19. 重庆八中将于2017年整体搬迁至渝北空港新城,新校园工程建设正在如火如荼的进行.经工程部管理人员同意,四位同学前往工地进行社会实践活动.如图,A、B、C是三个建筑原材料存放点,点B、C分别位于点A的正北和正东方向,AC=400米.四人分别测得∠C的度数如表:甲
乙
丙
丁
∠C(单位:度)
34
36
38
40
他们又调查了各点的建筑材料存放量,并绘制了下列尚不完整的统计如图、如图:
 (1)、求表中∠C度数的平均数 ;(2)、求A处的建筑原材料存放量,并将如图补充完整;(3)、用(1)中的 作为∠C的度数,要将A处的全部建筑原材料沿道路AB运到B处,已知运1方建筑原材料每米的费用为0.1元,求运完全部建筑原材料所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)20. 如图,点 A,B,C,D 依次在同一条直线上,点 E,F 分别在直线 AD 的两侧,已知 BE//CF,∠A=∠D,AE=DF.
(1)、求表中∠C度数的平均数 ;(2)、求A处的建筑原材料存放量,并将如图补充完整;(3)、用(1)中的 作为∠C的度数,要将A处的全部建筑原材料沿道路AB运到B处,已知运1方建筑原材料每米的费用为0.1元,求运完全部建筑原材料所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)20. 如图,点 A,B,C,D 依次在同一条直线上,点 E,F 分别在直线 AD 的两侧,已知 BE//CF,∠A=∠D,AE=DF.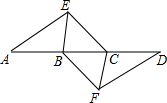 (1)、求证:四边形 BFCE 是平行四边形.(2)、若 AD=10,EC=3,∠EBD=60°,当四边形 BFCE是菱形时,求 AB 的长.21. 如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2 .过点D作DF∥BC,交AB的延长线于点F.
(1)、求证:四边形 BFCE 是平行四边形.(2)、若 AD=10,EC=3,∠EBD=60°,当四边形 BFCE是菱形时,求 AB 的长.21. 如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2 .过点D作DF∥BC,交AB的延长线于点F.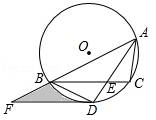 (1)、求证:DF为⊙O的切线;(2)、若∠BAC=60°,DE= ,求图中阴影部分的面积.22. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)、求证:DF为⊙O的切线;(2)、若∠BAC=60°,DE= ,求图中阴影部分的面积.22. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.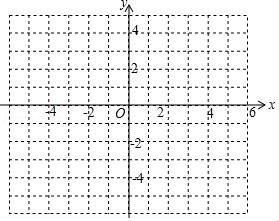 (1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.
(1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.