辽宁省朝阳市2019届九年级数学中考模拟试卷（3月）

试卷更新日期：2019-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各式中，不相等的是（）

A、 ${(- 3)}^{2}$ 和 $- 3^{2}$ B、 ${(- 3)}^{2}$ 和 $3^{2}$ C、 ${(- 2)}^{3}$ 和 $- 2^{3}$ D、 $| - 2 |^{3}$ 和 $| - 2^{3} |$

查看试题解析
2. 如图，直线a∥b，AC⊥AB，AC交直线b于点C，∠1＝55°，则∠2的度数是（）

A、35° B、25° C、65° D、50°

查看试题解析
3. 下列图形是轴对称图形的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 若 $3 a^{m + 2} b 与 \frac{1}{2} {ab}^{n - 1}$ 是同类项，则 $m + n = ($ $)$

A、 $- 2$ B、2 C、1 D、 $- 1$

查看试题解析
5. 小宁同学根据全班同学的血型绘制了如图所示的扇形统计图，该班血型为A型的有20人，那么该班血型为AB型的人数为（）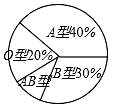

A、2人 B、5人 C、8人 D、10人

查看试题解析
6. 八年级（2）班学生积极参加献爱心活动，该班50名学生的捐款情况统计如表，则该班学生捐款金额的平均数和中位数分别是（）

金额/元

5

10

20

50

100

人数

4

16

15

9

6

A、20.6元和10元 B、20.6元和20元 C、30.6元和10元 D、30.6元和20元

查看试题解析
7. 如图， $⊙ P$ 的半径为5， $A 、 B$ 是圆上任意两点，且 $A B = 6$ ，以 $A B$ 为边作正方形 $A B C D$ （点 $D 、 P$ 在直线 $A B$ 两侧）.若 $A B$ 边绕点 $P$ 旋转一周，则 $C D$ 边扫过的面积为（）

A、 $5 π$ B、 $6 π$ C、 $8 π$ D、 $9 π$

查看试题解析
8. “凤鸣”文学社在学校举行的图书共享仪式上互赠图书，每个同学都把自己的图书向本组其他成员赠送一本，某组共互赠了210本图书，如果设该组共有x名同学，那么依题意，可列出的方程是（）

A、x（x+1）＝210 B、x（x﹣1）＝210 C、2x（x﹣1）＝210 D、 $\frac{1}{2}$ x（x﹣1）＝210

查看试题解析
9. 若0＜m＜2，则关于x的一元二次方程﹣（x+m）（x+3m）＝3mx+37根的情况是（）

A、无实数根 B、有两个正根 C、有两个根，且都大于﹣3m D、有两个根，其中一根大于﹣m

查看试题解析
10. 矩形 $A B C D$ 中， $A D = 2 A B = 2 \sqrt{2}$ ， $E$ 是 $A D$ 的中点， $R t ∠ F E G$ 顶点与点 $E$ 重合，将 $∠ F E G$ 绕点 $E$ 旋转，角的两边分别交 $A B ， B C$ （或它们的延长线）于点 $M ， N$ ，设 $∠ A M E = α (0 ° < α < 90 °)$ ，有下列结论：① $B M = C N$ ；② $A M + C N = \sqrt{2}$ ；③ $S_{Δ E M N} = \frac{1}{{sin}^{2} α}$ ，其中正确的是（）

A、① B、②③ C、①③ D、①②③

查看试题解析

二、填空题

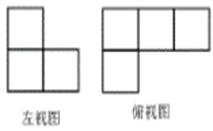
11. 现在网购越来越多地成为人们的一种消费方式，天猫和淘宝的支付交易额突破67000000000元，将67000000000元用科学记数法表示为.

查看试题解析
12. 一个不透明的袋子中装有4个红球、2个黑球，它们除颜色外其余都相同，从中任意搞出3球，则事件“摸出的球至少有1个红球”是事件(填“必然”、 “随机”或“不可能”)

查看试题解析
13. 不等式组 ${\begin{matrix} 8 x > 48 \\ 2 (x + 8) < 34 \end{matrix}$ 的解集为．

查看试题解析
14. 如图是由一些大小相同的小正方体组成的简单几何体的左视图和俯视图，符合条件的几何体有种.

查看试题解析
15. 菱形OBCD在平面直角坐标系中的位置如图所示，顶点B（2，0），∠DOB=60°，点E坐标为（0，﹣ $\sqrt{3}$ ），点P是对角线OC上一个动点，则EP+BP最短的最短距离为.

查看试题解析
16. 如图，在平面直角坐标系中，反比例函数 $y = \frac{2}{x}$ （x＞0）与正比例函数y=kx、 $y = \frac{x}{k}$ （k＞1）的图象分别交于点A、B，若∠AOB＝45°，则△AOB的面积是.

查看试题解析

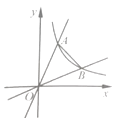
三、解答题

17. 计算： ${(\sqrt{5} - π)}^{0} - 6 tan 30^{0} + {(\frac{1}{2})}^{- 2} + | 1 - \sqrt{3} |$ .

查看试题解析
18. 解方程： $\frac{x}{x - 1} - \frac{2}{x} = 1$ ．

查看试题解析

19. 某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个.随机抽取了部分学生的听写结果，绘制成如下的图表.

组别	正确字数x	人数
A	0≤x＜8	10
B	8≤x＜16	15
C	16≤x＜24	25
D	24≤x＜32	m
E	32≤x＜40	n

根据以上信息完成下列问题：

(1)、统计表中的m＝， n＝，并补全条形统计图；

(2)、扇形统计图中“C组”所对应的圆心角的度数是；

(3)、已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，请你估计该校本次听写比赛不合格的学生人数.

查看试题解析

20. 某公园的人工湖边上有一座山，山顶上有一直竖的建筑物 $C D$ ，高为10米.某校数学兴趣小组的同学为了测量山的高度 $D E$ ，在公园找了一水平地面，在 $A$ 处测得建筑物点 $D$ （即山顶）的仰角为 $35 °$ ，沿水平方向前进20米到达 $B$ 点，测得建筑物顶部 $C$ 点的仰角为 $45 °$ ，求山的高度 $D E$ .（结果精确到1米，参考数据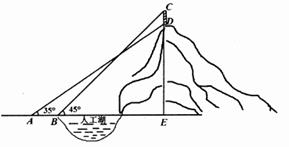： $sin 35 ° \approx \frac{7}{12}$ ， $cos 35 ° \approx \frac{5}{6}$ ， $tan 35 ° \approx \frac{7}{10}$ ）

查看试题解析
21. 在一次数学活动中，黑板上画着如图所示的图形，活动前老师在准备的四张卡片（大小、颜色、形状相同）的正面上分别写有如下四个等式中的一个等式：① $A B = C D$ ；② $A D / / B C$ ；③ $A B / / C D$ ；④ $∠ A = ∠ C$ ；小英同学闭上眼睛从四张卡片中随机抽出一张，再从剩下的卡片中随机抽出另一张，请结合图形回答下列问题：

(1)、当抽得②和④时，用②和④作条件能否判定四边形是平行四边形，请说明理由；

(2)、请你用树状图或表格表示抽取两张卡片上的条件的所有可能出现的结果（用序号表示）并求以已经抽取的两张卡片上的条件为已知，使四边形不能构成平行四边形的概率.

查看试题解析
22. 如图， $A B$ 为 $⊙ O$ 直径， $C$ 是 $⊙ O$ 上一点， $C O ⊥ A B$ 于点 $O$ ，弦 $C D$ 与 $A B$ 交于点 $F$ .过点 $D$ 作 $⊙ O$ 的切线交 $A B$ 的延长线于点 $E$ ，过点 $A$ 作 $⊙ O$ 的切线交 $E D$ 的延长线于点 $G$ .

(1)、求证： $Δ E F D$ 为等腰三角形；

(2)、若 $O F ： O B = 1 ： 3$ ， $⊙ O$ 的半径为3，求 $A G$ 的长.

查看试题解析
23. 某商品的进价为每件50元．当售价为每件70元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：

(1)、若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；

(2)、当降价多少元时，每星期的利润最大？最大利润是多少？

查看试题解析
24. 在正方形ABCD中，AB＝8，点P在边CD上，tan∠PBC＝ $\frac{3}{4}$ ，点Q是在射线BP上的一个动点，过点Q作AB的平行线交射线AD于点M，点R在射线AD上，使RQ始终与直线BP垂直.

(1)、如图1，当点R与点D重合时，求PQ的长；

(2)、如图2，试探索： $\frac{R M}{M Q}$ 的比值是否随点Q的运动而发生变化？若有变化，请说明你的理由；若没有变化，请求出它的比值；

(3)、如图3，若点Q在线段BP上，设PQ＝x，RM＝y，求y关于x的函数关系式，并写出它的定义域.

查看试题解析
25. 如图，直线AB和抛物线的交点是A（0，﹣3），B（5，9），已知抛物线的顶点D的横坐标是2.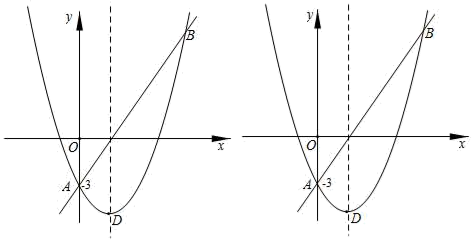

(1)、求抛物线的解析式及顶点坐标；

(2)、在x轴上是否存在一点C，与A，B组成等腰三角形？若存在，求出点C的坐标，若不在，请说明理由；

(3)、在直线AB的下方抛物线上找一点P，连接PA，PB使得△PAB的面积最大，并求出这个最大值.

查看试题解析

金额/元	5	10	20	50	100
人数	4	16	15	9	6