陕西省西安市周至县2019届数学中考一模试卷
试卷更新日期:2019-07-23 类型:中考模拟
一、单选题
-
1. 实数 的相反数是( )
A、﹣ B、 C、﹣ D、2. 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )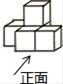 A、
A、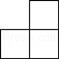 B、
B、 C、
C、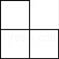 D、
D、 3. 下列计算正确的是( )A、y2+y2=2y4 B、y7+y4=y11 C、y2•y2+y4=2y4 D、y2•(y4)2=y184. 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )
3. 下列计算正确的是( )A、y2+y2=2y4 B、y7+y4=y11 C、y2•y2+y4=2y4 D、y2•(y4)2=y184. 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )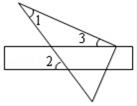 A、20° B、30° C、50° D、80°5. 已知y与x成正比例,且x=3时,y=2,则y=3时,x的值为( )A、 B、 C、2 D、126. 等腰三角形的一个外角是100°,则它的顶角的度数为( )A、80° B、80°或20° C、20° D、80°或50°7. 若一次函数y=2x+6与y=kx的图象的交点纵坐标为4,则k的值是( )A、﹣4 B、﹣2 C、2 D、48. 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1 , 连结AD1 , BC1 . 若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B;②当x=1时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形;④s= (x﹣2)2(0<x<2)。其中正确的有( )
A、20° B、30° C、50° D、80°5. 已知y与x成正比例,且x=3时,y=2,则y=3时,x的值为( )A、 B、 C、2 D、126. 等腰三角形的一个外角是100°,则它的顶角的度数为( )A、80° B、80°或20° C、20° D、80°或50°7. 若一次函数y=2x+6与y=kx的图象的交点纵坐标为4,则k的值是( )A、﹣4 B、﹣2 C、2 D、48. 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1 , 连结AD1 , BC1 . 若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B;②当x=1时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形;④s= (x﹣2)2(0<x<2)。其中正确的有( ) A、1 个 B、2 个 C、3 个 D、4 个9. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A、1 个 B、2 个 C、3 个 D、4 个9. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( ) A、2 B、8 C、 D、210. 已知二次函数y=ax2+bx+c的图像经过点(0,m)、(4、m)、(1,n),若n<m,则( )A、a>0且4a+b=0 B、a<0且4a+b=0 C、a>0且2a+b=0 D、a<0且2a+b=0
A、2 B、8 C、 D、210. 已知二次函数y=ax2+bx+c的图像经过点(0,m)、(4、m)、(1,n),若n<m,则( )A、a>0且4a+b=0 B、a<0且4a+b=0 C、a>0且2a+b=0 D、a<0且2a+b=0二、填空题
-
11. 不等式1﹣2x<6的负整数解是 .12. 用科学计算器计算:﹣tan65°≈ (精确到0.01)13. 如图,过原点的直线l与反比例函数y=﹣ 的图象交于M,N两点,若MO=5,则ON=.根据图象猜想,线段MN的长度的最小值.
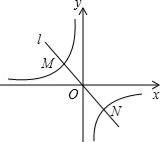 14. 如图,在平面直角坐标系中,等边三角形ABC的顶点B、C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M.当边AB恰平分线段ON时,则AN=.
14. 如图,在平面直角坐标系中,等边三角形ABC的顶点B、C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M.当边AB恰平分线段ON时,则AN=.
三、解答题
-
15. 计算:2cos30°+ - -( )-216. 计算: ÷(x+ )17. 如图,△ABC中AB=AC,请你利用尺规在BC边上求一点P,使△ABC~△PAC不写画法,(保留作图痕迹).
 18. “低碳生活,绿色出行”是我们倡导的一种生活方式,某校为了解学生对共享单车的使用情况,随机抽取部分学生进行问卷调查,并将这次调查的结果绘制了以下两幅不完整的统计图.
18. “低碳生活,绿色出行”是我们倡导的一种生活方式,某校为了解学生对共享单车的使用情况,随机抽取部分学生进行问卷调查,并将这次调查的结果绘制了以下两幅不完整的统计图.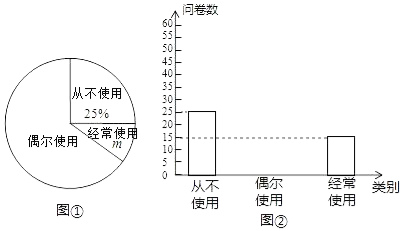
根据所给信息,解答下列问题:
(1)、m=;(2)、补全条形统计图;(3)、这次调查结果的众数是;(4)、已知全校共3000名学生,请估计“经常使用”共享单车的学生大约有多少名?19. 如图,在平行四边形ABCD中,E、F是对角线BD上的两点,且BF=DE.求证:AE∥CF.
 20. 如图,河对岸有一路灯杆AB,在灯光下,小亮在点D处测得自己的影长DF=3m,沿BD方向从D后退4米到G处,测得自己的影长GH=5,如果小亮的身高为1.7m,求路灯杆AB的高度.
20. 如图,河对岸有一路灯杆AB,在灯光下,小亮在点D处测得自己的影长DF=3m,沿BD方向从D后退4米到G处,测得自己的影长GH=5,如果小亮的身高为1.7m,求路灯杆AB的高度. 21. 下表中有两种移动电话计费方式.
21. 下表中有两种移动电话计费方式.月使用费 元
主叫限定时间
主叫超时费
被叫
方式一
49
100
免费
方式二
69
150
免费
设一个月内主叫通话为t分钟 是正整数 .
(1)、当 时,按方式一计费为元;按方式二计费为元;(2)、当 时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;(3)、当 时,请直接写出省钱的计费方式?22. 甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.(1)、若由甲挑一名选手打第一场比赛,选中乙的概率是多少?(直接写出答案)(2)、任选两名同学打第一场,请用树状图或列表法求恰好选中甲、乙两位同学的概率。23. 如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.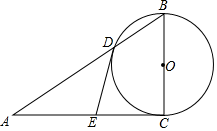 (1)、求证:∠A=∠ADE;(2)、若AD=8,DE=5,求BC的长.24. 抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).
(1)、求证:∠A=∠ADE;(2)、若AD=8,DE=5,求BC的长.24. 抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).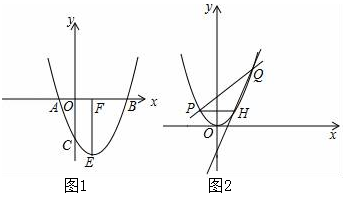 (1)、求抛物线的解析式;(2)、如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.(3)、如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.25. 如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)、求抛物线的解析式;(2)、如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.(3)、如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.25. 如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG (1)、判断CG与⊙O的位置关系,并说明理由;(2)、求证:2OB2=BC•BF;(3)、如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.
(1)、判断CG与⊙O的位置关系,并说明理由;(2)、求证:2OB2=BC•BF;(3)、如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.