辽宁省辽阳市2019届数学中考模拟试卷(3月)
试卷更新日期:2019-07-23 类型:中考模拟
一、单选题
-
1. 给出四个数0, ,π,﹣1,其中最小的是( )A、0 B、 C、π D、﹣12. 在正方形、矩形、菱形、平行四边形中,其中是中心对称图形的个数为( )A、1 B、2 C、3 D、43. 下列等式成立的是( )A、(a+4)(a﹣4)=a2﹣4 B、2a2﹣3a=﹣a C、a6÷a3=a2 D、(a2)3=a64. 如图所示是机器零件的立体图,从上面看到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 要调查下面的问题:①调查某种灯泡的使用寿命.②调查你们班学生早餐是否有喝牛奶的习惯.③调查全国中学生的节水意识。④查某学校七年级学生的视力情况.其中适合采用普查的是( )A、①③ B、②④ C、①②④ D、②③④6. “五一”江北水城文化旅游节期间,几名同学包租一辆面包车前去旅游,面包车的租价为180元,出发时又增加了两名同学,结果每个同学比原来少摊了3元钱车费,设原来参加游览的同学共x人,则所列方程为( )A、 B、 C、 D、7. 一组数据按从大到小排列为2,4,8,x,10,14.若这组数据的中位数为9,则这组数据的众数为( )A、6 B、8 C、9 D、108. 若一次函数 ( 为常数且 )满足如表,则方程 的解是( )A、 B、 C、 D、9. 如图, 平分 于点 ,则 ( )
5. 要调查下面的问题:①调查某种灯泡的使用寿命.②调查你们班学生早餐是否有喝牛奶的习惯.③调查全国中学生的节水意识。④查某学校七年级学生的视力情况.其中适合采用普查的是( )A、①③ B、②④ C、①②④ D、②③④6. “五一”江北水城文化旅游节期间,几名同学包租一辆面包车前去旅游,面包车的租价为180元,出发时又增加了两名同学,结果每个同学比原来少摊了3元钱车费,设原来参加游览的同学共x人,则所列方程为( )A、 B、 C、 D、7. 一组数据按从大到小排列为2,4,8,x,10,14.若这组数据的中位数为9,则这组数据的众数为( )A、6 B、8 C、9 D、108. 若一次函数 ( 为常数且 )满足如表,则方程 的解是( )A、 B、 C、 D、9. 如图, 平分 于点 ,则 ( )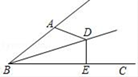 A、 B、 C、 D、10. 甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( )
A、 B、 C、 D、10. 甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
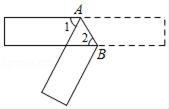
11. 禽流感病毒的形状一般为球形,直径大约为0.000000102m,将0.000000102用科学记数法表示为 .12. 分解因式: =.13. 如图,把一张长方形纸片沿 折叠后,若 ,则 的大小为度.
 14. 如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是 .
14. 如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是 .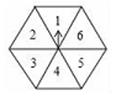 15. 如图,点 是⨀ 上的三点,若 ,则 的度数是.
15. 如图,点 是⨀ 上的三点,若 ,则 的度数是.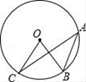 16. 如图,湖心岛上有一凉亭B,在凉亭B的正东湖边有一棵大树A,在湖边的C处测得B在北偏西45°方向上,测得A在北偏东30°方向上,又测得A、C之间的距离为100米,则A、B之间的距离是米(结果保留根号形式).
16. 如图,湖心岛上有一凉亭B,在凉亭B的正东湖边有一棵大树A,在湖边的C处测得B在北偏西45°方向上,测得A在北偏东30°方向上,又测得A、C之间的距离为100米,则A、B之间的距离是米(结果保留根号形式). 17. 如图,一次函数 的图象与 轴、 轴分别交于点 ,点 在 轴上,要使 是以AB为腰的等腰三角形,那么点 的坐标是.
17. 如图,一次函数 的图象与 轴、 轴分别交于点 ,点 在 轴上,要使 是以AB为腰的等腰三角形,那么点 的坐标是. 18. 如图,正方形 的顶点 的坐标为 为正方形 的中心;以正方形 的对角线 为边,在 的右侧作正方形 为正方形 的中心;再以正方形 的对角线 为边,在 的右侧作正方形 为正方形 的中心;再以正方形 的对角线 为边,在 的右侧作正方形 为正方形 的中心:…;按照此规律继续下去,则点 的坐标为.
18. 如图,正方形 的顶点 的坐标为 为正方形 的中心;以正方形 的对角线 为边,在 的右侧作正方形 为正方形 的中心;再以正方形 的对角线 为边,在 的右侧作正方形 为正方形 的中心;再以正方形 的对角线 为边,在 的右侧作正方形 为正方形 的中心:…;按照此规律继续下去,则点 的坐标为.
三、解答题
-
19.(1)、计算: .(2)、先化简,再求值: ,其中 .20. “校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
 (1)、接受问卷调査的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为°;(2)、请补全条形统计图;(3)、若该中学共有学生1600人,请根据上述调查结果,估计该学校学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;(4)、若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.21. 某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
(1)、接受问卷调査的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为°;(2)、请补全条形统计图;(3)、若该中学共有学生1600人,请根据上述调查结果,估计该学校学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;(4)、若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.21. 某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
18000元
第二周
4台
10台
31000元
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)、求A、B两种型号的空调的销售单价;(2)、若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?22. 直线y=kx+b与反比例函数 (x>0)的图象分别交于点A(m,4)和点B(8,n),与坐标轴分别交于点C和点D. (1)、求直线AB的解析式;(2)、观察图象,当x>0时,直接写出 的解集;(3)、若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.23. 如图,点C是以AB为直径的⊙O上一点,CP与AB的延长线相交于点P,已知AB=2BP,AC= BP.
(1)、求直线AB的解析式;(2)、观察图象,当x>0时,直接写出 的解集;(3)、若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.23. 如图,点C是以AB为直径的⊙O上一点,CP与AB的延长线相交于点P,已知AB=2BP,AC= BP. (1)、求证:PC与⊙O相切;(2)、若⊙O的半径为3,求阴影部分弓形的面积.24. 某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量 万件 与销售单价 元 之间符合一次函数关系,其图象如图所示.
(1)、求证:PC与⊙O相切;(2)、若⊙O的半径为3,求阴影部分弓形的面积.24. 某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量 万件 与销售单价 元 之间符合一次函数关系,其图象如图所示. (1)、求y与x的函数关系式;(2)、物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润 最大?最大利润是多少?25. 已知如图 1,在 中, , ,点 在 上, 交 于 ,点 是 的中点.
(1)、求y与x的函数关系式;(2)、物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润 最大?最大利润是多少?25. 已知如图 1,在 中, , ,点 在 上, 交 于 ,点 是 的中点.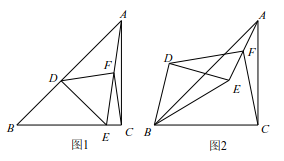 (1)、写出线段 与线段 的关系并证明;(2)、如图,将 绕点 逆时针旋转 ,其它条件不变,线段 与线段 的关系是否变化,写出你的结论并证明;(3)、将 绕点 逆时针旋转一周,如果 ,直接写出线段 的范围.26. 如图,抛物线 与 轴交于点 和 ,与 轴交于点 .
(1)、写出线段 与线段 的关系并证明;(2)、如图,将 绕点 逆时针旋转 ,其它条件不变,线段 与线段 的关系是否变化,写出你的结论并证明;(3)、将 绕点 逆时针旋转一周,如果 ,直接写出线段 的范围.26. 如图,抛物线 与 轴交于点 和 ,与 轴交于点 .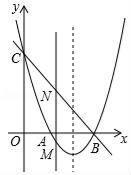 (1)、求抛物线的解析式;(2)、若点 是抛物线上在 轴下方的动点,过 作 轴交直线 于点 ,求线段 的最大值;(3)、 是抛物线对称轴上一点, 是抛物线上一点,是否存在以 , , , 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若点 是抛物线上在 轴下方的动点,过 作 轴交直线 于点 ,求线段 的最大值;(3)、 是抛物线对称轴上一点, 是抛物线上一点,是否存在以 , , , 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.