辽宁省本溪市高新技术开发区2019届数学中考一模试卷
试卷更新日期:2019-07-23 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、3x2﹣7x=﹣4x B、﹣3y2+4y2=y2 C、(﹣a2)3=a6 D、(﹣a)2•a4=﹣a62. 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列事件中必然发生的事件是( )A、一个图形平移后所得的图形与原来的图形不全等 B、不等式的两边同时乘以一个数,结果仍是不等式 C、200件产品中有5件次品,从中任意抽取6件,至少有一件是正品 D、随意翻到一本书的某页,这页的页码一定是偶数4. 若a>b成立,则下列不等式成立的是( )A、﹣a>﹣b B、﹣a+1>﹣b+1 C、﹣(a﹣1)>﹣(b﹣1) D、a﹣1>b﹣15. 关于反比例函数y=﹣ 的图象,下列说法正确的是( )A、经过点(﹣1,﹣4) B、当x<0时,图象在第二象限 C、无论x取何值时,y随x的增大而增大 D、图象是轴对称图形,但不是中心对称图形6. 一个两位数,它的十位数字是3,个位数字是抛掷一枚质地均匀的骰子(六个面分别标有数字1﹣6)朝上一面的数字,任意抛掷这枚骰子一次,得到的两位数是3的倍数的概率等于( )A、 B、 C、 D、7. 某足球生产厂计划生产4800个足球,在生产完1200个后,采用了新技术,工作效率比原计划提高了20%,结果共用了21天完成全部任务.设原计划每天生产x个足球,根据题意可列方程为( )A、 =21 B、 =21 C、 =21 D、 =218. 已知关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是( )A、k<﹣2 B、k<2 C、k>2 D、k<2且k≠19. 已知原点是抛物线y=(m+1)x2的最低点,则m的取值范围是( )A、m<﹣1 B、m<1 C、m>﹣1 D、m>﹣210. 已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
3. 下列事件中必然发生的事件是( )A、一个图形平移后所得的图形与原来的图形不全等 B、不等式的两边同时乘以一个数,结果仍是不等式 C、200件产品中有5件次品,从中任意抽取6件,至少有一件是正品 D、随意翻到一本书的某页,这页的页码一定是偶数4. 若a>b成立,则下列不等式成立的是( )A、﹣a>﹣b B、﹣a+1>﹣b+1 C、﹣(a﹣1)>﹣(b﹣1) D、a﹣1>b﹣15. 关于反比例函数y=﹣ 的图象,下列说法正确的是( )A、经过点(﹣1,﹣4) B、当x<0时,图象在第二象限 C、无论x取何值时,y随x的增大而增大 D、图象是轴对称图形,但不是中心对称图形6. 一个两位数,它的十位数字是3,个位数字是抛掷一枚质地均匀的骰子(六个面分别标有数字1﹣6)朝上一面的数字,任意抛掷这枚骰子一次,得到的两位数是3的倍数的概率等于( )A、 B、 C、 D、7. 某足球生产厂计划生产4800个足球,在生产完1200个后,采用了新技术,工作效率比原计划提高了20%,结果共用了21天完成全部任务.设原计划每天生产x个足球,根据题意可列方程为( )A、 =21 B、 =21 C、 =21 D、 =218. 已知关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是( )A、k<﹣2 B、k<2 C、k>2 D、k<2且k≠19. 已知原点是抛物线y=(m+1)x2的最低点,则m的取值范围是( )A、m<﹣1 B、m<1 C、m>﹣1 D、m>﹣210. 已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )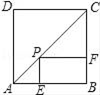 A、
A、 B、
B、 C、
C、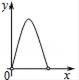 D、
D、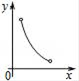
二、填空题
-
11. 禽流感病毒的形状一般为球形,直径大约为0.000000102m,将0.000000102用科学记数法表示为 .12. 因式分解:m3n﹣9mn= .13. 已知一组数据1,2,3,5,x的平均数是3,则这组数据的方差是 .14. 如图,有一条直的宽纸带,按图方式折叠,则∠α的度数等于.
 15. 如果样本x1 , x2 , x3 , …,xn的平均数为5,那么样本x1+2,x2+2,x3+2,…xn+2的平均数是16. 已知 - =1,则 的值等于17. 把一个长方形纸片按如图所示折叠,若量得∠AOD′=36°,则∠D′OE的度数为 .
15. 如果样本x1 , x2 , x3 , …,xn的平均数为5,那么样本x1+2,x2+2,x3+2,…xn+2的平均数是16. 已知 - =1,则 的值等于17. 把一个长方形纸片按如图所示折叠,若量得∠AOD′=36°,则∠D′OE的度数为 .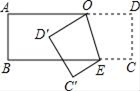 18. 在直角坐标系中,直线l:y= x﹣ 与x轴交于点B1 , 以OB1为边长作等边△A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边△A2A1B2 , 过点A2作A1B2平行于x轴,交直线l于点B3 , 以A2B3为边长作等边△A3A2B3 , …,则等边△A2017A2018B2018的边长是 .
18. 在直角坐标系中,直线l:y= x﹣ 与x轴交于点B1 , 以OB1为边长作等边△A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边△A2A1B2 , 过点A2作A1B2平行于x轴,交直线l于点B3 , 以A2B3为边长作等边△A3A2B3 , …,则等边△A2017A2018B2018的边长是 .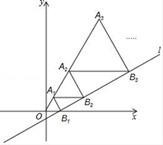
三、解答题
-
19. 先化简,再求值:(2﹣ )÷ ,其中x= ﹣3.20. 已知:如图,在平行四边形ABCD中,M、N分别是AD和BC的中点.
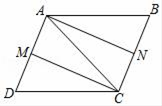 (1)、求证:四边形AMCN是平行四边形;(2)、若AC=CD,求证四边形AMCN是矩形;(3)、若∠ACD=90°,求证四边形AMCN是菱形;(4)、若AC=CD,∠ACD=90°,求证四边形AMCN是正方形.21. 某校开展了以“责任、感恩”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图,
(1)、求证:四边形AMCN是平行四边形;(2)、若AC=CD,求证四边形AMCN是矩形;(3)、若∠ACD=90°,求证四边形AMCN是菱形;(4)、若AC=CD,∠ACD=90°,求证四边形AMCN是正方形.21. 某校开展了以“责任、感恩”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图,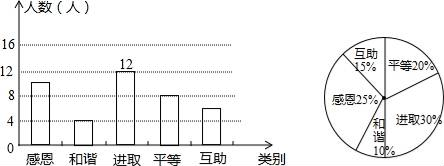 (1)、该班有人,学生选择“和谐”观点的有人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是度;(2)、如果该校有360名初三学生,利用样本估计选择“感恩”观点的初三学生约有人;(3)、如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).22. 如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)、该班有人,学生选择“和谐”观点的有人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是度;(2)、如果该校有360名初三学生,利用样本估计选择“感恩”观点的初三学生约有人;(3)、如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).22. 如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E. (1)、试判断DE与⊙O的位置关系,并说明理由;(2)、过点D作DF⊥AB于点F,若BE=3 ,DF=3,求图中阴影部分的面积.23. 如图1,滑动调节式遮阳伞的立柱 垂直于地面 , 为立柱上的滑动调节点,伞体的截面示意图为 , 为 中点, , , , .当点 位于初始位置 时,点 与 重合(图2).根据生活经验,当太阳光线与 垂直时,遮阳效果最佳.
(1)、试判断DE与⊙O的位置关系,并说明理由;(2)、过点D作DF⊥AB于点F,若BE=3 ,DF=3,求图中阴影部分的面积.23. 如图1,滑动调节式遮阳伞的立柱 垂直于地面 , 为立柱上的滑动调节点,伞体的截面示意图为 , 为 中点, , , , .当点 位于初始位置 时,点 与 重合(图2).根据生活经验,当太阳光线与 垂直时,遮阳效果最佳. (1)、上午10:00时,太阳光线与地面的夹角为 (图3),为使遮阳效果最佳,点 需从 上调多少距离?(结果精确到 )(2)、中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点 在(1)的基础上还需上调多少距离?(结果精确到 )
(1)、上午10:00时,太阳光线与地面的夹角为 (图3),为使遮阳效果最佳,点 需从 上调多少距离?(结果精确到 )(2)、中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点 在(1)的基础上还需上调多少距离?(结果精确到 )(参考数据: , , , , )
24. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.销售单价x(元)
3.5
5.5
销售量y(袋)
280
120
(1)、请直接写出y与x之间的函数关系式;(2)、如果每天获得160元的利润,销售单价为多少元?(3)、设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?25. 已知如图 1,在 中, , ,点 在 上, 交 于 ,点 是 的中点.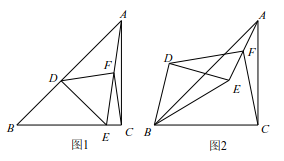 (1)、写出线段 与线段 的关系并证明;(2)、如图,将 绕点 逆时针旋转 ,其它条件不变,线段 与线段 的关系是否变化,写出你的结论并证明;(3)、将 绕点 逆时针旋转一周,如果 ,直接写出线段 的范围.26. 如图1,已知抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于点C,顶点为D,连接BC
(1)、写出线段 与线段 的关系并证明;(2)、如图,将 绕点 逆时针旋转 ,其它条件不变,线段 与线段 的关系是否变化,写出你的结论并证明;(3)、将 绕点 逆时针旋转一周,如果 ,直接写出线段 的范围.26. 如图1,已知抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于点C,顶点为D,连接BC (1)、点G是直线BC上方抛物线上一动点(不与B、C重合),过点G作y轴的平行线交直线BC于点E,作GF⊥BC于点F,点M、N是线段BC上两个动点,且MN=EF,连接DM、GN.当△GEF的周长最大时,求DM+MN+NG的最小值;(2)、如图2,连接BD,点P是线段BD的中点,点Q是线段BC上一动点,连接DQ,将△DPQ沿PQ翻折,且线段D′P的中点恰好落在线段BQ上,将△AOC绕点O逆时针旋转60°得到△A′OC′,点T为坐标平面内一点,当以点Q、A′、C′、T为顶点的四边形是平行四边形时,求点T的坐标.
(1)、点G是直线BC上方抛物线上一动点(不与B、C重合),过点G作y轴的平行线交直线BC于点E,作GF⊥BC于点F,点M、N是线段BC上两个动点,且MN=EF,连接DM、GN.当△GEF的周长最大时,求DM+MN+NG的最小值;(2)、如图2,连接BD,点P是线段BD的中点,点Q是线段BC上一动点,连接DQ,将△DPQ沿PQ翻折,且线段D′P的中点恰好落在线段BQ上,将△AOC绕点O逆时针旋转60°得到△A′OC′,点T为坐标平面内一点,当以点Q、A′、C′、T为顶点的四边形是平行四边形时,求点T的坐标.