江苏无锡2019届数学中考模拟试卷
试卷更新日期:2019-07-23 类型:中考模拟
一、单选题
-
1. 6的倒数是( )A、 ﹣6 B、6 C、 D、﹣2. 如图是某几何体的三视图,则与该三视图相对应的几何体是( )
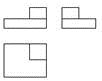 A、
A、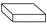 B、
B、 C、
C、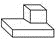 D、
D、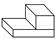 3. 在下列运算中,计算正确的是( )A、m2+m2=m4 B、(m+1)2=m2+1 C、(3mn2)2=6m2n4 D、2m2n÷(﹣mn)=﹣2m4. 若线段AB∥x轴且AB=3,点A的坐标为(2,1),则点B的坐标为( )A、(5,1) B、(﹣1,1) C、(5,1)或(﹣1,1) D、(2,4)或(2,﹣2)5. 关于反比例函数 的图象,下列说法正确的是 )A、图象经过点 B、两个分支分布在第二、四象限 C、当 时,y随x的增大而减小 D、两个分支关于x轴成轴对称6. 为鼓励同学们阅读经典,了解同学们课外阅读经典名著的情况,在某年级随机抽查了20名同学每期的课外阅读名著的情况,调查结果如表:
3. 在下列运算中,计算正确的是( )A、m2+m2=m4 B、(m+1)2=m2+1 C、(3mn2)2=6m2n4 D、2m2n÷(﹣mn)=﹣2m4. 若线段AB∥x轴且AB=3,点A的坐标为(2,1),则点B的坐标为( )A、(5,1) B、(﹣1,1) C、(5,1)或(﹣1,1) D、(2,4)或(2,﹣2)5. 关于反比例函数 的图象,下列说法正确的是 )A、图象经过点 B、两个分支分布在第二、四象限 C、当 时,y随x的增大而减小 D、两个分支关于x轴成轴对称6. 为鼓励同学们阅读经典,了解同学们课外阅读经典名著的情况,在某年级随机抽查了20名同学每期的课外阅读名著的情况,调查结果如表:课外名著阅读量(本)
8
9
10
11
12
学生数
3
3
4
6
4
则关于这20名周学课外阅读经典名著的情况,下列说法正确的是( )
A、中位数是10 B、平均数是10.25 C、众数是12 D、以上说法均不符合题意7. 已知 是关于x的一元二次方程 的一个根,则k的值为( )A、3 B、 C、2 D、8. 如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为( )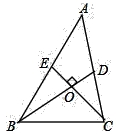 A、4 B、8 C、12 D、169. 如图,半径为3的⊙A的 与▱ABCD的边BC相切于点C,交AB于点E,则 的长为( )
A、4 B、8 C、12 D、169. 如图,半径为3的⊙A的 与▱ABCD的边BC相切于点C,交AB于点E,则 的长为( )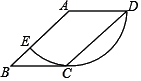 A、 B、 C、 D、10. 如图,一次函数y=﹣x与二次函数为y=ax2+bx+c的图象相交于点M,N,则关于x的一元二次方程ax2+(b+1)x+c=0的根的情况是( )
A、 B、 C、 D、10. 如图,一次函数y=﹣x与二次函数为y=ax2+bx+c的图象相交于点M,N,则关于x的一元二次方程ax2+(b+1)x+c=0的根的情况是( ) A、有两个不相等的实数根 B、有两个相等的实数 C、没有实数根 D、以上结论都正确
A、有两个不相等的实数根 B、有两个相等的实数 C、没有实数根 D、以上结论都正确二、填空题
-
11. 现在网购越来越多地成为人们的一种消费方式,在2018年的“双11”网上促销活动中天猫和淘宝的支付交易额突破220000000000元,将数字220000000000用科学记数法表示为 .12. 函数y= 中,自变量x的取值范围是.13. 关于x,y的二元一次方程组 ,则4x2﹣4xy+y2的值为.14. 将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为.
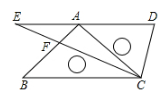 15. 一次函数 ,当 时, ,那么不等式 的解集为.16. 如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小等于度.
15. 一次函数 ,当 时, ,那么不等式 的解集为.16. 如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小等于度.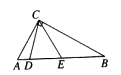 17. 如图,在长方形ABCD中,DC=6cm,在DC上存在一点E,沿直线AE把△ADE折叠,使点D恰好落在BC边上的点F处,若△ABF的面积为24cm2 , 那么折叠的△ADE的面积为.
17. 如图,在长方形ABCD中,DC=6cm,在DC上存在一点E,沿直线AE把△ADE折叠,使点D恰好落在BC边上的点F处,若△ABF的面积为24cm2 , 那么折叠的△ADE的面积为.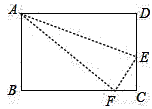 18. 在平面直角坐标系中,已知 、 ,B为y轴上的动点,以AB为边构造 ,使点C在x轴上, 为BC的中点,则PM的最小值为.
18. 在平面直角坐标系中,已知 、 ,B为y轴上的动点,以AB为边构造 ,使点C在x轴上, 为BC的中点,则PM的最小值为.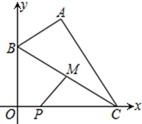
三、解答题
-
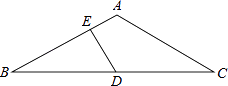
19. 计算:20. 解不等式组: .21. 如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AB于E,求EB:EA的值.
 22. 某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
22. 某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题: (1)、本次共调查了名学生;(2)、将图1的统计图补充完整;(3)、已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.23. 小明坐于堤边垂钓,如图,河堤 的坡角为 , 长为 米,钓竿 的倾斜角是 ,其长为 米,若 与钓鱼线 的夹角为 ,求浮漂 与河堤下端 之间的距离.
(1)、本次共调查了名学生;(2)、将图1的统计图补充完整;(3)、已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.23. 小明坐于堤边垂钓,如图,河堤 的坡角为 , 长为 米,钓竿 的倾斜角是 ,其长为 米,若 与钓鱼线 的夹角为 ,求浮漂 与河堤下端 之间的距离.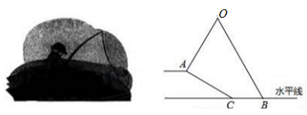 24. 如图,一次函数
24. 如图,一次函数 的图象分别交 x 轴、 轴于
的图象分别交 x 轴、 轴于  两点,
两点,  为 的中点,
为 的中点,  轴于点 ,延长
轴于点 ,延长  交反比例函数
交反比例函数  的图象于点
的图象于点  ,且
,且 
 (1)、求 的值;(2)、连结
(1)、求 的值;(2)、连结 求证:四边形
求证:四边形  是菱形. 25. “绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
是菱形. 25. “绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:村庄
清理养鱼网箱人数/人
清理捕鱼网箱人数/人
总支出/元
A
15
9
57000
B
10
16
68000
(1)、若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;(2)、在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?26. 如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.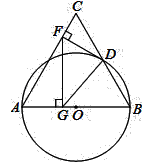 (1)、求证:DF是⊙O的切线;(2)、若AB=12,求FG的长;(3)、在(2)问条件下,求点D到FG的距离.27. 如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上.
(1)、求证:DF是⊙O的切线;(2)、若AB=12,求FG的长;(3)、在(2)问条件下,求点D到FG的距离.27. 如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上. (1)、求m、n;(2)、向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;(3)、记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′,C,D为顶点的三角形与△ABC相似.
(1)、求m、n;(2)、向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;(3)、记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′,C,D为顶点的三角形与△ABC相似.