江苏苏州市相城区2019届数学中考模拟试卷

试卷更新日期：2019-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 在﹣6，0，2.5，|﹣3|这四个数中，最大的数是（）

A、﹣6 B、0 C、2.5 D、|﹣3|

查看试题解析
2. 适合条件∠A＝ $\frac{1}{2}$ ∠B＝ $\frac{1}{3}$ ∠C的△ABC是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形

查看试题解析
3. 我县人口约为530060人，用科学记数法可表示为（）

A、53006×10人 B、5.3006×10⁵人 C、53×10⁴人 D、0.53×10⁶人

查看试题解析
4. 小王抛一枚质地均匀的硬币，连续抛4次，硬币均正面朝上落地，如果他再抛第5次，那么硬币正面朝上的概率为（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
5. 若一个圆锥的底面半径为3cm，母线长为5cm，则这个圆锥的全面积为（）

A、15π cm² B、24π cm² C、39π cm² D、48π cm²

查看试题解析
6. 已知α、β是方程x²﹣2x﹣4＝0的两个实数根，则α³+8β+6的值为（）

A、﹣1 B、2 C、22 D、30

查看试题解析
7. 如图，某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向，船向西航行20海里到达B处，测得电视塔A在船的西北方向，若要轮船离电视塔最近，则还需向西航行（）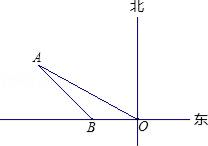

A、 $10 (\sqrt{3} + 1)$ 海里 B、 $10 (\sqrt{3} - 1)$ 海里 C、 $20 (\sqrt{3} + 1)$ 海里 D、 $20 (\sqrt{3} - 1)$ 海里

查看试题解析
8. 如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值为（）

A、 $\frac{\sqrt{10}}{5}$ B、 $\sqrt{2}$ C、 $\frac{1}{2}$ D、2

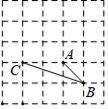查看试题解析
9. 已知一次函数的图象与直线y＝﹣x+1平行，且过点（8，2），那么此一次函数的解析式为（）

A、y＝﹣x﹣2 B、y＝﹣x﹣6 C、y＝﹣x+10 D、y＝﹣x﹣1

查看试题解析
10. 若二次函数y＝﹣2x²+k与y＝2x²﹣ $\frac{1}{2}$ 的图象的顶点重合，则下列结论：①两图象的形状相同；②两图象的对称轴相同；③y＝﹣2x²+k的顶点为(0，- $\frac{1}{2}$ )；④方程﹣2x²+k＝0没有实根；⑤y＝﹣2x²+k有最大值为﹣ $\frac{1}{2}$ .其中正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 因式分解：16x⁴﹣y⁴＝.

查看试题解析
12. 平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分，则该平行四边形的周长为．

查看试题解析
13. 已知小丽某周每天的睡眠时间为(单位：h)：8，9，7，9，7，8，8，则她该周睡眠时间的众数为.

查看试题解析
14. 在函数 $y = \frac{\sqrt{x - 4}}{x + 1}$ 中，自变量x的取值范围是．

查看试题解析
15. 关于x的一元二次方程kx²+2x﹣1=0有两个不相等的实数根，则k的取值范围是．

查看试题解析
16. ⊙ $O$ 的半径为 $1$ ，弦 $A B = \sqrt{2}$ ，弦 $A C = \sqrt{3}$ ，则 $∠ B A C$ 度数为．

查看试题解析
17. 如图，在平面直角坐标系xOy中，反比例函数y＝﹣ $\frac{4}{x}$ 在第二象限的图象上有一点A，过点A作AB⊥x轴于点B，则S_△_AOB＝.

查看试题解析
18. 如图，线段AB＝10，点P在线段AB上，在AB的同侧分别以AP、BP为边长作正方形APCD和BPEF，点M、N分别是EF、CD的中点，则MN的最小值是.

查看试题解析

三、解答题

19. 计算：（﹣ $\sqrt{3}$ ）⁰﹣|﹣3|+（﹣1）²⁰¹⁵+（ $\frac{1}{2}$ ）^﹣¹ ．

查看试题解析
20. 解不等式： $\frac{2 - 3 x}{3}$ ﹣ $\frac{x - 1}{2}$ ≤1

查看试题解析
21. 先化简代数式1﹣ $\frac{x - 1}{x}$ ÷ $\frac{x^{2} - 1}{x^{2} + 2 x}$ ，并从﹣1，0，1，3中选取一个合适的代入求值．

查看试题解析
22. 已知 ${(a - 2)}^{2} + \sqrt{b + 4} + | c - 3 | = 0$ ，求方程 $a x + \frac{b}{x} = c + 4$ 的解.

查看试题解析
23. 已知平行四边形ABCD中，如图，对角线AC和BD相交于点O，AC=10，BD=8.

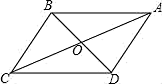(1)、若AC⊥BD，试求四边形ABCD的面积；

(2)、若AC与BD的夹角∠AOD=60°，求四边形ABCD的面积.

查看试题解析
24. 某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：

(1)、在这次调查中，喜欢篮球项目的同学有人，在扇形统计图中，“乒乓球”的百分比为%，如果学校有800名学生，估计全校学生中有人喜欢篮球项目.

(2)、请将条形统计图补充完整.

(3)、在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队，请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.

查看试题解析
25. 如图，等腰直角△POA的直角顶点P在反比例函数 $y = \frac{4}{x}$ (x＞0)的图象上，A点在x轴正半轴上，求A点坐标.

查看试题解析

26. 某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调，如表是近两周的销售情况：

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	3台	5台	18000元
第二周	4台	10台	31000元

(进价、售价均保持不变，利润＝销售总收入进货成本)

(1)、求A、B两种型号的空调的销售单价；

(2)、若超市准备用不多于54000元的金额再采购这两种型号的空调共30台，求A种型号的空调最多能采购多少台？

查看试题解析

27. 已知，四边形ABCD中，E是对角线AC上一点，DE＝EC，以AE为直径的⊙O与边CD相切于点D，点B在⊙O上，连接OB．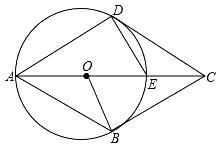

(1)、求证：DE＝OE；

(2)、若CD∥AB，求证：BC是⊙O的切线；

(3)、在（2）的条件下，求证：四边形ABCD是菱形．

查看试题解析
28. 已知，抛物线y＝ax²+ax+b(a≠0)与直线y＝2x+m有一个公共点M(1，0)，且a＜b．

(1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示)；

(2)、直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；

(3)、a＝﹣1时，直线y＝﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位(t＞0)，若线段GH与抛物线有两个不同的公共点，试求t的取值范围．

查看试题解析