江苏省无锡市锡山区东亭片八校2019届数学中考一模试卷
试卷更新日期:2019-07-23 类型:中考模拟
一、单选题
-
1. 2的相反数是A、 B、2 C、 D、2. 如图所示物体的俯视图是( )
 A、
A、 B、
B、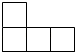 C、
C、 D、
D、 3. 计算(﹣ xy2)3 , 结果正确的是( )A、 x3y5 B、﹣ x3y6 C、 x3y6 D、﹣ x3y54. 方程 的解为A、 B、 C、 , D、 ,5. 在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是( )
3. 计算(﹣ xy2)3 , 结果正确的是( )A、 x3y5 B、﹣ x3y6 C、 x3y6 D、﹣ x3y54. 方程 的解为A、 B、 C、 , D、 ,5. 在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是( )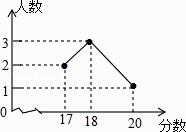 A、18,18,1 B、18,17.5,3 C、18,18,3 D、18,17.5,16. 关于反比例函数 的图象,下列说法正确的是 )A、图象经过点 B、两个分支分布在第二、四象限 C、当 时,y随x的增大而减小 D、两个分支关于x轴成轴对称7. 如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是( )A、10cm2 B、10πcm2 C、20cm2 D、20πcm28. 如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A、18,18,1 B、18,17.5,3 C、18,18,3 D、18,17.5,16. 关于反比例函数 的图象,下列说法正确的是 )A、图象经过点 B、两个分支分布在第二、四象限 C、当 时,y随x的增大而减小 D、两个分支关于x轴成轴对称7. 如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是( )A、10cm2 B、10πcm2 C、20cm2 D、20πcm28. 如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )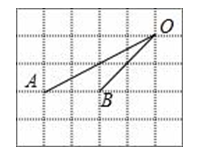 A、 B、 C、 D、9. 如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为( )
A、 B、 C、 D、9. 如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为( )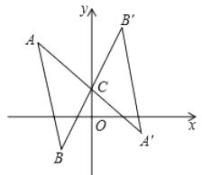 A、(-a,-b) B、(-a,-b-1) C、(-a,-b+1) D、(-a,-b+2)10. “如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A、(-a,-b) B、(-a,-b-1) C、(-a,-b+1) D、(-a,-b+2)10. “如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A、 B、 C、 D、二、填空题
-
11. 数据显示,今年高校毕业生规模达到727万人,比去年有所增加.数据727万人用科学记数法表示为人.12. 三张扑克牌中只有一张黑桃,三位同学依次抽取,第一位同学抽到黑桃的概率为.13. 直线 ,一块含 角的直角三角板如图放置, ,则 .
 14. 一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是 .
14. 一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是 .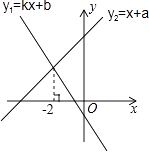 15. 如图,在△ABC中,AB=AC,∠A=40º,点D在AC上,BD=BC,则∠ABD的度数为.
15. 如图,在△ABC中,AB=AC,∠A=40º,点D在AC上,BD=BC,则∠ABD的度数为.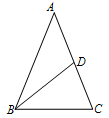 16. 如图,Rt△ABC中,∠ABC=90º,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为 .
16. 如图,Rt△ABC中,∠ABC=90º,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为 . 17. 在平面直角坐标系中,已知 、 ,B为y轴上的动点,以AB为边构造 ,使点C在x轴上, 为BC的中点,则PM的最小值为.
17. 在平面直角坐标系中,已知 、 ,B为y轴上的动点,以AB为边构造 ,使点C在x轴上, 为BC的中点,则PM的最小值为.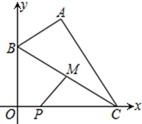
三、解答题
-
18.(1)、解方程: ;(2)、解不等式组: .19. 已知:如图,AB为⊙O的直径,⊙O过AC的中点D,DE⊥BC于点E.
 (1)、求证:DE为⊙O的切线;(2)、若DE=2,tanC= ,求⊙O的直径.20. 某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.(1)、甲、乙两种材料每千克分别是多少元?(2)、现工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?(3)、在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,才能使生产这批产品的成本最低?请直接写出方案.21. 已知:PA= ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)、求证:DE为⊙O的切线;(2)、若DE=2,tanC= ,求⊙O的直径.20. 某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.(1)、甲、乙两种材料每千克分别是多少元?(2)、现工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?(3)、在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,才能使生产这批产品的成本最低?请直接写出方案.21. 已知:PA= ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧. (1)、如图,当∠APB=45°时,求AB及PD的长;(2)、当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.22. 计算与化简(1)、(2)、23. 如图,平行四边形ABCD的对角线AC、BD,相交于点O,EF过点O且与AB、CD分别相交于点E、F,求证:AE=CF.
(1)、如图,当∠APB=45°时,求AB及PD的长;(2)、当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.22. 计算与化简(1)、(2)、23. 如图,平行四边形ABCD的对角线AC、BD,相交于点O,EF过点O且与AB、CD分别相交于点E、F,求证:AE=CF. 24. 某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m, 分别用 、 、 表示 ;田赛项目:跳远,跳高 分别用 、 表示 .(1)、该同学从5个项目中任选一个,恰好是田赛项目的概率为;(2)、该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.25. 某企业500名员工参加安全生产知识测试,成绩记为A,B,C,D,E共5个等级,为了解本次测试的成绩(等级)情况,现从中随机抽取部分员工的成绩(等级),统计整理并制作了如下的统计图:
24. 某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m, 分别用 、 、 表示 ;田赛项目:跳远,跳高 分别用 、 表示 .(1)、该同学从5个项目中任选一个,恰好是田赛项目的概率为;(2)、该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.25. 某企业500名员工参加安全生产知识测试,成绩记为A,B,C,D,E共5个等级,为了解本次测试的成绩(等级)情况,现从中随机抽取部分员工的成绩(等级),统计整理并制作了如下的统计图:
 (1)、求这次抽样调查的样本容量,并补全图①;(2)、如果测试成绩(等级)为A,B,C级的定为优秀,请估计该企业参加本次安全生产知识测试成绩(等级)达到优秀的员工的总人数.
(1)、求这次抽样调查的样本容量,并补全图①;(2)、如果测试成绩(等级)为A,B,C级的定为优秀,请估计该企业参加本次安全生产知识测试成绩(等级)达到优秀的员工的总人数.
