江苏省泰州市泰兴市黄桥教育联盟2019届数学中考一模试卷(3月)
试卷更新日期:2019-07-23 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列运算正确的是( )A、x﹣2x=x B、(xy)2=xy2 C、 × = D、(﹣ )2=43. 下列图形中是中心对称图形的是( )A、
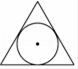 B、
B、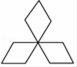 C、
C、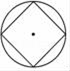 D、
D、 4. 某小组 8 名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
4. 某小组 8 名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( )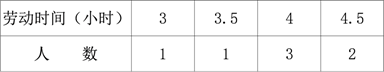 A、中位数是 4,众数是 4 B、中位数是 3.5,众数是 4 C、平均数是 3.5,众数是 4 D、平均数是4,众数是3.55. 如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
A、中位数是 4,众数是 4 B、中位数是 3.5,众数是 4 C、平均数是 3.5,众数是 4 D、平均数是4,众数是3.55. 如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )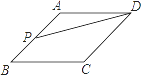 A、
A、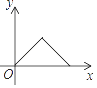 B、
B、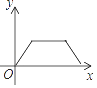 C、
C、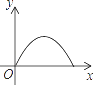 D、
D、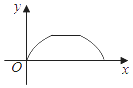
二、填空题
-
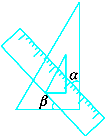
6. 函数y= 中自变量x的取值范围是.7. 因式分解:x3-9x=.8. 袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为 ,则这个袋中白球大约有个.9. 将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是.
 10.
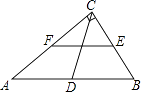
10.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=3cm,则EF=cm.
 11. 如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC= .
11. 如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC= .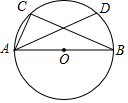 12. 平面直角坐标系中一点P(m﹣3,1﹣2m)在第三象限,则m的取值范围是.13. 如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为.
12. 平面直角坐标系中一点P(m﹣3,1﹣2m)在第三象限,则m的取值范围是.13. 如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为.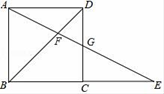 14. 如图,矩形ABCD的边AB与x轴平行,顶点A的坐标为(2,1),点B与点D都在反比例函数 的图象上,则矩形ABCD的周长为.
14. 如图,矩形ABCD的边AB与x轴平行,顶点A的坐标为(2,1),点B与点D都在反比例函数 的图象上,则矩形ABCD的周长为.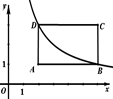 15. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.则CG=.
15. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.则CG=.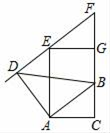
三、解答题
-
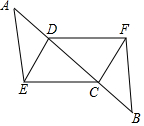
16.(1)、计算:( -1)0+(﹣1)﹣2﹣4sin60°+ ,(2)、解方程: + =117. 随着互联网的迅速发展,某购物网站的年销售额从2013年的200万元增加到2015年的392万元.求该购物网站平均每年销售额增长的百分率.18. 已知:如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.
 19. 如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据: , , 结果精确到0.1小时)
19. 如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据: , , 结果精确到0.1小时) 20. 某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
20. 某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:频数
频率
体育
40
0.4
科技
25
a
艺术
b
0.15
其它
20
0.2
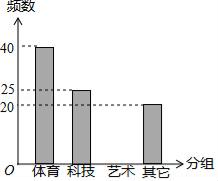
请根据上图完成下面题目:
(1)、总人数为人,a= , b=.(2)、请你补全条形统计图.(3)、若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?21. 一个不透明的袋子中,装有标号分别为1、-1、2的三个小球,他们除标号不同外,其余都完全相同;(1)、搅匀后,从中任意取一个球,标号为正数的概率是 ;(2)、搅匀后,从中任取一个球,标号记为k,然后放回搅匀再取一个球,标号记为b,求直线y=kx+b经过一、二、三象限的概率.22. 如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.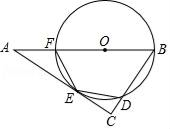 (1)、求证:∠C=90°;(2)、当BC=3,sinA= 时,求AF的长.23. 如图,A(4,3)是反比例函数y= 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y= 的图象于点P.
(1)、求证:∠C=90°;(2)、当BC=3,sinA= 时,求AF的长.23. 如图,A(4,3)是反比例函数y= 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y= 的图象于点P.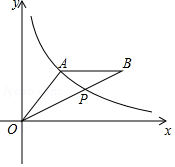 (1)、求反比例函数y= 的表达式;(2)、求点B的坐标;(3)、求△OAP的面积.24. 已知二次函数 与一次函数 ,令W= .(1)、若 、 的函数图象交于x轴上的同一点.
(1)、求反比例函数y= 的表达式;(2)、求点B的坐标;(3)、求△OAP的面积.24. 已知二次函数 与一次函数 ,令W= .(1)、若 、 的函数图象交于x轴上的同一点.①求 的值;
②当 为何值时,W的值最小,试求出该最小值;
(2)、当 时,W随x的增大而减小.①求
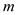 的取值范围;
的取值范围;②求证: .
25. 如图 (1)、问题发现
(1)、问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
① 的值为;
②∠AMB的度数为.
(2)、类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断 的值及∠AMB的度数,并说明理由;
(3)、拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB= ,请直接写出当点C与点M重合时AC的长.