湖北省武汉市东湖高新区2019届九年级数学中考模拟试卷

试卷更新日期：2019-07-22 类型：中考模拟

进入出卷网下载

一、单选题

1. 我市2018年的最高气温为39℃，最低气温为零下7℃，则计算2018年温差列式正确的（）

A、（+39）﹣（﹣7） B、（+39）+（+7） C、（+39）+（﹣7） D、（+39）﹣（+7）

查看试题解析
2. 无论a取何值时，下列分式一定有意义的是（）

A、 $\frac{a^{2} + 1}{a^{2}}$ B、 $\frac{a + 1}{a^{2}}$ C、 $\frac{a^{2} - 1}{a + 1}$ D、 $\frac{a - 1}{a^{2} + 1}$

查看试题解析
3. 下列运算正确的是（　　）

A、﹣a²b+2a²b=a²b B、2a﹣a=2 C、3a²+2a²=5a⁴ D、2a+b=2ab

查看试题解析
4. 在一个不透明的布袋中装有黄、白两种颜色的球共40个，除颜色外其他都相同，小王通过多次摸球试验后发现，摸到黄球的频率稳定在0.35左右，则布袋中黄球可能有（）

A、12个 B、14个 C、18个 D、28个

查看试题解析
5. 如（x+a）与（x+3）的乘积中不含x的一次项，则a的值为（）

A、3 B、﹣3 C、1 D、﹣1

查看试题解析
6. 点M（1，2）关于y轴对称点的坐标为（）

A、（﹣1，2） B、（﹣1，﹣2） C、（1，﹣2） D、（2，﹣1）

查看试题解析
7. 由一些大小相同的小正方体搭成的几何体的左视图和俯视图，如图所示，则搭成该几何体的小正方体的个数最多是（）

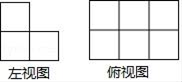A、7 B、8 C、9 D、10

查看试题解析
8. 某校八年级两个班，各选派10名学生参加学校举行的“汉字听写”大赛．各参赛选手成绩的数据分析如下表所示，则以下判断错误的是（）
班级
平均数
中位数
众数
方差
八（1）班
94
93
94
12
八（2）班
95
95.5
93
8.4

A、八（2）班的总分高于八（1）班 B、八（2）班的成绩比八（1）班稳定 C、八（2）班的成绩集中在中上游 D、两个班的最高分在八（2）班

查看试题解析
9. 如图，在平面直角坐标系中，已知⊙A经过点E，B，O，C且点O为坐标原点，点C在y轴上，点E在x轴上，A（﹣3，2），则cos∠OBC的值为（）

A、 $\frac{2}{3}$ B、 $\frac{3 \sqrt{13}}{13}$ C、 $\frac{2 \sqrt{13}}{13}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
10. 如图，AD和AC分别是⊙O的直径和弦，且∠CAD＝30°，OB⊥AD，交AC于点B，若OB＝5，则BC的长是（）

A、5 B、5 $\sqrt{3}$ C、5 $\sqrt{6}$ ﹣10 D、10﹣5 $\sqrt{3}$

查看试题解析

二、填空题

11. 计算 $\sqrt{12}$ ﹣9 $\sqrt{\frac{1}{3}}$ 的结果是．

查看试题解析
12. 若m+n=1，mn=2，则 $\frac{1}{m} + \frac{1}{n}$ 的值为．

查看试题解析
13. 为了弘扬中华传统文化，营造书香校园文化氛围，2017年12月11日，兴义市新电学校举行中华传统文化知识大赛活动该学校从三名男生和两名女生中选出两名同学担任本次活动的主持人，则选出的恰为一男一女的概率是

查看试题解析
14. 将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，若∠ABE＝20°，则∠DBC为度.

查看试题解析
15. 如图，在菱形ABCD中，∠BAD＝120°，CE⊥AD，且CE＝BC，连接BE交对角线AC于点F，则∠EFC＝°

查看试题解析
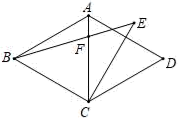16. 已知二次函数y=x²﹣4x+k的图象的顶点在x轴下方，则实数k的取值范围是．

查看试题解析

三、解答题

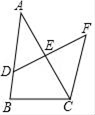
17. 解方程组： ${\begin{matrix} 4 x - 3 y = 11 \\ 2 x + y = 13 \end{matrix}$ .

查看试题解析
18. 如图，点D是AB上一点，E是AC的中点，连接DE并延长到F，使得DE=EF，连接CF.求证：FC∥AB.

查看试题解析

19. 某校八（1）班同学为了解2018年姜堰某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，请解答以下问题：

月均用水量x（t）	频数（户）	频率
0＜x≤5	6	0.12
5＜x≤10	12	0.24
10＜x≤15	m	0.32
15＜x≤20	10	n
20＜x≤25	4	0.08
25＜x≤30	2	0.04

(1)、本次调查采用的调杳方式是（填“普査”或“抽样调查”），样本容量是；

(2)、补全频数分布直方图：

(3)、若将月均用水量的频数绘成扇形统计图，则月均用水量“15＜x≤20”的圆心角度数是；

(4)、若该小区有5000户家庭，求该小区月均用水量超过20t的家庭大约有多少户？

查看试题解析

20. 一个进行数值转换的运行程序如图所示，从“输入实数x”到“结果是否大于0”称为“一次操作”

(1)、判断：
①当输入x＝3后，程序操作仅进行一次就停止.

②当输入x为负数时，无论x取何负数，输出的结果总比输入数大.

(2)、探究：是否存在正整数x，使程序能进行两次操作，并且输出结果小于12？若存在，请求出所有符合条件的x的值；若不存在，请说明理由.

查看试题解析
21. 如图，以AB为直径作半圆O，点C是半圆上一点，∠ABC的平分线交⊙O于E，D为BE延长线上一点，且∠DAE＝∠FAE.

(1)、求证：AD为⊙O切线；

(2)、若sin∠BAC＝ $\frac{3}{5}$ ，求tan∠AFO的值.

查看试题解析
22. 矩形AOBC中，OB＝8，OA＝4.分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系.F是BC边上一个动点（不与B，C重合），过点F的反比例函数y＝ $\frac{k}{x}$ （k＞0）的图象与边AC交于点E.

(1)、当点F运动到边BC的中点时，求点E的坐标；

(2)、连接EF、AB，求证：EF∥AB；

(3)、如图2，将△CEF沿EF折叠，点C恰好落在边OB上的点G处，求此时反比例函数的解析式.

查看试题解析
23. △ABC中，BC＝12，高AD＝8，矩形EFGH的一边GH在BC上，顶点E、F分别在AB、AC上，AD与EF交于点M.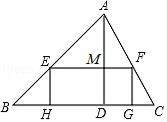

(1)、求证： $\frac{AM}{AD} = \frac{EF}{BC}$ ；

(2)、设EF＝x，EH＝y，写出y与x之间的函数表达式；

(3)、设矩形EFGH的面积为S，求S与x之间的函数表达式，并写出S的最大值.

查看试题解析
24. 如图，在平面直角坐标系中有一直角三角形AOB，O为坐标原点，OA＝1，tan∠BAO＝3，将此三角形绕原点O逆时针旋转90°，得到△DOC，抛物线y＝ax²+bx+c经过点A、B、C．

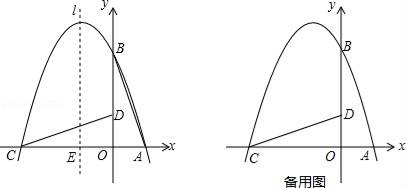(1)、求抛物线的解析式；

(2)、若点P是第二象限内抛物线上的动点，其横坐标为t，设抛物线对称轴l与x轴交于一点E，连接PE，交CD于F，求以C、E、F为顶点三角形与△COD相似时点P的坐标．

查看试题解析

班级	平均数	中位数	众数	方差
八（1）班	94	93	94	12
八（2）班	95	95.5	93	8.4