湖北省武汉市2019届数学中考模拟试卷(4月)
试卷更新日期:2019-07-22 类型:中考模拟
一、单选题
-
1. 计算-5+1的结果为( )A、-6 B、-4 C、4 D、62. 若代数式 在实数范围内有意义,则实数 的取值范围为A、 B、 C、 D、3. 计算2a2+3a2的结果是( )A、5a4 B、6a2 C、6a4 D、5a24. 如图,两个转盘A,B都被分成了3个全等的扇形,在每一扇形内均标有不同的自然数,固定指针,同时转动转盘A,B,两个转盘停止后观察两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向上边的扇形).小明每转动一次就记录数据,并算出两数之和,其中“和为7”的频数及频率如下表:
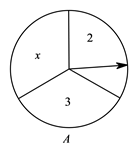


如果实验继续进行下去,根据上表数据,出现“和为7”的频率将稳定在它的概率附近,估计出现“和为7”的概率为( )
A、0.33 B、0.34 C、0.20 D、0.355. 计算(x-1)(x-2)的结果为( )A、x2+2 B、x2-3x+2 C、x2-3x-3 D、x2-2x+26. 在坐标系中,将点P( -2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P’的坐标( )A、(2,4) B、(1,5) C、(1,-3) D、(-5,5)7. 下列左图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则该几何体的主视图为( ) A、
A、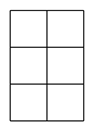 B、
B、 C、
C、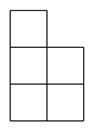 D、
D、 8. 统计学校排球队员的年龄,发现有12、13、14、15等四种年龄,统计结果如下表:
8. 统计学校排球队员的年龄,发现有12、13、14、15等四种年龄,统计结果如下表:年龄(岁)
12
13
14
15
人数(个)
2
4
6
8
根据表中信息可以判断该排球队员年龄的平均数、众数、中位数分别为( )
A、13、15、14 B、14、15、14 C、13.5、15、14 D、15、15、159. 如图,在矩形纸片ABCD中,已知AB= ,BC=1,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE折叠,得到多边形AFGE,点B,C的对应点分别为点F、G.在点E从点C移动到点D的过程中,则点F运动的路径长为( )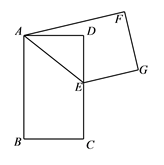 A、π B、 π C、 π D、 π
A、π B、 π C、 π D、 π二、填空题
-
10. 化简: = .11. 计算 的结果是.12. 口袋中装有4个小球,其中红球3个,黄球1个,从中随机摸出两球,都是红球的概率为.13. 如图,▱ABCD中,E是BA的中点,连接DE,将△DAE沿DE折叠,使点A落在▱ABCD内部的点F处.若∠CBF=25°,则∠FDA的度数为.
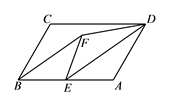 14. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC、BD,若S四边形ABCD=18,则BD的最小值为.
14. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC、BD,若S四边形ABCD=18,则BD的最小值为.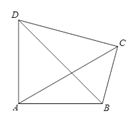 15. 已知抛物线y=x2上一点A,以A为顶点作抛物线C:y=x2+bx+c,点B(2,yB)为抛物线C上一点,当点A在抛物线y=x2上任意移动时,则yB的取值范围是.
15. 已知抛物线y=x2上一点A,以A为顶点作抛物线C:y=x2+bx+c,点B(2,yB)为抛物线C上一点,当点A在抛物线y=x2上任意移动时,则yB的取值范围是.三、解答题
-
16. 解方程组: .17. 如图,点D是AB上一点,DF交AC于点E, DE=FE,FC∥AB.求证:AE=CE.
 18. 雾霾天气时常会影响市民的生活质量.前不久,我校气候先锋队的同学对“雾霾天气的主要成因”随机调查了部分市民,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察分析并回答下列问题.
18. 雾霾天气时常会影响市民的生活质量.前不久,我校气候先锋队的同学对“雾霾天气的主要成因”随机调查了部分市民,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察分析并回答下列问题.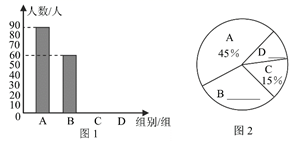 (1)、本次被调查的市民共有多少人?(2)、补全条形统计图,并将扇形统计图B、D两区域对应的圆心角的度数分别为;(3)、若武汉城区有1000万人口,请估计持有A或B种观点的市民共约有多少人?
(1)、本次被调查的市民共有多少人?(2)、补全条形统计图,并将扇形统计图B、D两区域对应的圆心角的度数分别为;(3)、若武汉城区有1000万人口,请估计持有A或B种观点的市民共约有多少人?组别
雾霾天气的主要成因
百分比
A
工业污染
45%
B
汽车尾气排放
m
C
炉烟气排放
15%
D
其他(滥砍滥伐等)
n
19. 武商量贩销售A,B两种商品,售出4件B种商品所得利润为400元;售出3件A种商品和5件B种商品所得利润为1100元.(1)、求每件A种商品和每件B种商品售出后所得利润分别为多少元;(2)、由于需求量大,A,B两种商品很快售完,武商量贩决定再一次购进A,B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么武商量贩至少需购进多少件A种商品?20. 如图,△ABC内接于⊙O,AB=AC,BO的延长线交AC于点D.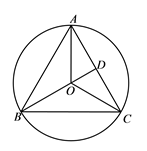 (1)、求证:△OAD∽△ABD;(2)、记△AOB、△AOD、△COD的面积分别为Sl、S2、S3 , 若S22=S1·S3 , 求 的值.21. 如图,双曲线y1 = 与直线y2=4x交于点A(1,m)、B.
(1)、求证:△OAD∽△ABD;(2)、记△AOB、△AOD、△COD的面积分别为Sl、S2、S3 , 若S22=S1·S3 , 求 的值.21. 如图,双曲线y1 = 与直线y2=4x交于点A(1,m)、B. (1)、直接写出:①k的值为;②m的值为;(2)、点C是双曲线y1= (x>0)上异于点A的一点,作直线AC、BC与x轴分别交于E、D.
(1)、直接写出:①k的值为;②m的值为;(2)、点C是双曲线y1= (x>0)上异于点A的一点,作直线AC、BC与x轴分别交于E、D.①若OA=OC,求DE的值;
22. 如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.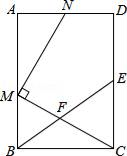 (1)、当F为BE中点时,求证:AM=CE;(2)、若 =2,求 的值;(3)、若 =n,当n为何值时,MN∥BE?23. 如图1,抛物线y=x2+(m﹣2)x﹣2m(m>0)与x轴交于A、B两点(A在B左边),与y轴交于点C.连接AC、BC,D为抛物线上一动点(D在B、C两点之间),OD交BC于E点.
(1)、当F为BE中点时,求证:AM=CE;(2)、若 =2,求 的值;(3)、若 =n,当n为何值时,MN∥BE?23. 如图1,抛物线y=x2+(m﹣2)x﹣2m(m>0)与x轴交于A、B两点(A在B左边),与y轴交于点C.连接AC、BC,D为抛物线上一动点(D在B、C两点之间),OD交BC于E点.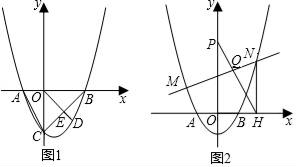 (1)、若△ABC的面积为8,求m的值;(2)、在(1)的条件下,求 的最大值;(3)、如图2,直线y=kx+b与抛物线交于M、N两点(M不与A重合,M在N左边),连MA,作NH⊥x轴于H,过点H作HP∥MA交y轴于点P,PH交MN于点Q,求点Q的横坐标.
(1)、若△ABC的面积为8,求m的值;(2)、在(1)的条件下,求 的最大值;(3)、如图2,直线y=kx+b与抛物线交于M、N两点(M不与A重合,M在N左边),连MA,作NH⊥x轴于H,过点H作HP∥MA交y轴于点P,PH交MN于点Q,求点Q的横坐标.