湖北省荆州石首市2018-2019学年数学中考一模试卷

试卷更新日期：2019-07-22 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中最小的是（）

A、﹣π B、1 C、 $- \sqrt{3}$ D、0

查看试题解析
2. 麒麟区是云南省曲靖市政府所在地，位于云南省东部，滇东高原中部，南盘江上游，截止2018年末麒麟区有常住人口约76万人，76万这个数字用科学记数法表示为（）

A、0.76×10⁶ B、7.6×10⁵ C、76×10⁴ D、7.6×10⁶

查看试题解析
3. 如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是（）

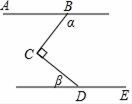A、α+β＝180° B、α+β＝90° C、β＝3α D、α﹣β＝90°

查看试题解析
4. 为了调查某校同学的体质健康状况，随机抽查了若干名同学的每天锻炼时间如表：

每天锻炼时间（分钟）

20

40

60

90

学生数

2

3

4

1

则关于这些同学的每天锻炼时间，下列说法错误的是（）

A、众数是60 B、平均数是21 C、抽查了10个同学 D、中位数是50

查看试题解析
5. 下列各式属于最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{x^{2} + 1}$ C、 $\sqrt{y^{2}}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
6. 如图，在△ABC中，AB＝AC，AB的垂直平分线交边AB于D点，交边AC于E点，若△ABC与△EBC的周长分别是40，24，则AB为（）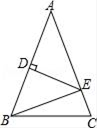

A、8 B、12 C、16 D、20

查看试题解析
7. 在如图所示的2018年1月份的月历表中，任意框出表中竖列上三个相邻的数，这三个数的和可能是（）

A、23 B、51 C、65 D、75

查看试题解析
8. 从电线杆离地面8米处拉一根长为10m的缆绳，这条缆绳在地面的固定点距离电线杆底部有（）m．

A、2 B、4 C、6 D、8

查看试题解析
9. 下图是从不同的方向看一个物体得到的平面图形，则该物体的形状是（）

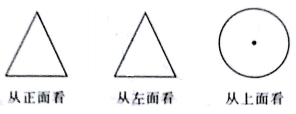A、圆锥 B、圆柱 C、三棱锥 D、三棱柱

查看试题解析
10. 抛物线y＝x²﹣9与x轴交于A、B两点，点P在函数y＝ $\frac{\sqrt{3}}{x}$ 的图象上，若△PAB为直角三角形，则满足条件的点P的个数为（）

A、2个 B、3个 C、4个 D、6个

查看试题解析

二、填空题

11. 计算： $\sqrt{16}$ +（π﹣3）⁰﹣（﹣ $\frac{1}{3}$ ）^﹣²＝.

查看试题解析
12. 计算：① $\sqrt{1^{3}}$ ② $\sqrt{1^{3} + 2^{3}}$ ③ $\sqrt{1^{3} + 2^{3} + 3^{3}}$ ④ $\sqrt{1^{3} + 2^{3} + 3^{3} + 4^{3}}$ ，观察你计算的结果，用你发现的规律直接写出下面式子的值 $\sqrt{1^{3} + 2^{3} + 3^{3} + \dots + 28^{3}}$ =

查看试题解析
13. 关于x的方程 $\frac{2 x - a}{x - 2}$ ＝1的解是正数，则a的取值范围是．

查看试题解析
14. 用形状大小完全相同的等边三角形和正方形按如图所示的规律拼图案，即从第2个图案开始每个图案比前一个图案多4个等边三角形和1个正方形，则第n个图案中等边三角形的个数为个.

查看试题解析
15. 将函数y＝3x+1的图象平移，使它经过点(1，1)，则平移后的函数表达式是．

查看试题解析
16. 已知点A、B、C、D均在圆上，AD∥BC，AC 平分∠BCD，∠ADC=120°，四边形的周长为10cm.，则∠ABC的度数为.

查看试题解析
17. 如图，在5×5的正方形网格中有一条线段AB，点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求：①仅用无刻度直尺，且不能用直尺中的直角；②保留必要的作图痕迹.

查看试题解析
18. 如图，在平面直角坐标系中，矩形OABC的顶点A、C分别在 $x$ 负半轴、 $y$ 正半轴上，点B在第二象限.将矩形OABC绕点O顺时针旋转，使点B落在 $y$ ，得到矩形ODEF，BC与OD相交于点M.若经过点M的反比例函数y= $\frac{k}{x}$ （x＜0）的图象交AB于点N，的图象交AB于点N， S_矩形OABC=32，tan∠DOE = $\frac{1}{2}$ ，N的长为.

查看试题解析

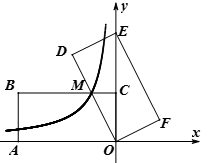
三、解答题

19.

(1)、解方程组： ${\begin{matrix} y = 2 x - 3 \\ 3 x + 2 y = 8 \end{matrix}$

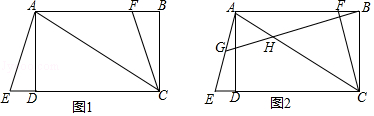
(2)、先化简，再求值： $\frac{x + 1}{x - 1}$ ﹣ $\frac{1}{x^{2} - 1}$ ÷ $\frac{1}{x + 1}$ ，其中x＝2．

查看试题解析
20. 如图1，在矩形ABCD中，AC为对角线，延长CD至点E使CE=CA，连接AE.F为AB上的一点，且BF=DE，连接FC.

(1)、若DE=1，CF= $2 \sqrt{2}$ ，求CD的长；

(2)、如图2，点G为线段AE的中点，连接BG交AC于H，若∠BHC+∠ABG=60°，求证：AF+CE= $\sqrt{3}$ AC.

查看试题解析
21. 为了解某中学学生课余生活情况，对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取 $n$ 名学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名学生只能选择其中一项）.并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息，解答下列问题：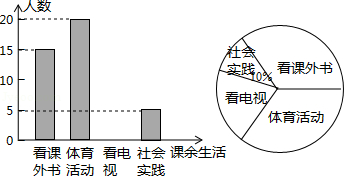

(1)、求n的值；

(2)、若该校学生共有1200人，试估计该校喜爱看电视的学生人数；

(3)、若调查到喜爱体育活动的4名学生中有3名男生和1名女生，现从这4名学生中任意抽取2名学生，求恰好抽到2名男生的概率.

查看试题解析
22. 如图，某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°，沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°.已知BC＝90米，且B、C、D在同一条直线上，山坡坡度i＝5：12.

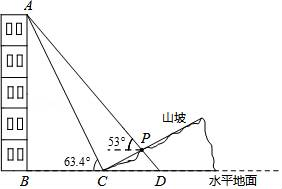(1)、求此人所在位置点P的铅直高度.(结果精确到0.1米)

(2)、求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)(测倾器的高度忽略不计，参考数据：tan53°≈ $\frac{4}{3}$ ，tan63.4°≈2)

查看试题解析
23. 已知关于x函数y＝(2﹣k)x²﹣2x+k

(1)、若此函数的图象与坐标轴只有2个交点，求k的值．

(2)、求证：关于x的一元二次方程(2﹣k)x²﹣2x+k＝0必有一个根是1．

查看试题解析
24. 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角(两边足够长)，用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB，BC两边)，设AB＝xm.

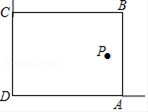(1)、若花园的面积为252m² ，求x的值；

(2)、若在P处有一棵树与墙CD，AD的距离分别是17m和6m，要将这棵树围在花园内(含边界，不考虑树的粗细)，求花园面积S的最大值.

查看试题解析
25. 已知直线l经过A(6，0)和B(0，12)两点，且与直线y＝x交于点C，点P(m，0)在x轴上运动．

(1)、求直线l的解析式；

(2)、过点P作l的平行线交直线y＝x于点D，当m＝3时，求△PCD的面积；

(3)、是否存在点P，使得△PCA成为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析

每天锻炼时间（分钟）	20	40	60	90
学生数	2	3	4	1