河南省平顶山市叶县2019届数学中考一模试卷(3月)
试卷更新日期:2019-07-22 类型:中考模拟
一、单选题
-
1. ﹣8的相反数是( )A、﹣8 B、 C、8 D、﹣2. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口44亿,这个数用科学记数法表示为( )A、44×108 B、4.4×109 C、4.4×108 D、4.4×10103. 第14届中国(深圳)国际茶产业博览会在深圳会展中心展出一只如图所示的紫砂壶,从不同方向看这只紫砂壶,你认为是从上面看到的效果图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列各运算中,计算正确的是( )A、a12÷a3=a4 B、(3a2)3=9a6 C、(a﹣b)2=a2﹣ab+b2 D、2a•3a=6a25. 一组数据-3,2,2,0,2,1的众数是( )A、-3 B、2 C、0 D、16. 游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽是红色游泳帽的2倍,设男孩有x人,女孩有y人,则下列方程组正确的是( )
4. 下列各运算中,计算正确的是( )A、a12÷a3=a4 B、(3a2)3=9a6 C、(a﹣b)2=a2﹣ab+b2 D、2a•3a=6a25. 一组数据-3,2,2,0,2,1的众数是( )A、-3 B、2 C、0 D、16. 游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽是红色游泳帽的2倍,设男孩有x人,女孩有y人,则下列方程组正确的是( ) A、 B、 C、 D、7. 一元二次方程x2﹣2kx+k2﹣k+2=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣2 B、k<﹣2 C、k<2 D、k>28. 将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于( )
A、 B、 C、 D、7. 一元二次方程x2﹣2kx+k2﹣k+2=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣2 B、k<﹣2 C、k<2 D、k>28. 将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于( )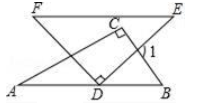 A、75° B、90° C、105° D、115°9. 如图,以矩形ABOD的两边OD、OB为坐标轴建立直角坐标系,若E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交OD于F点.若OF=1,FD=2,则G点的坐标为( )
A、75° B、90° C、105° D、115°9. 如图,以矩形ABOD的两边OD、OB为坐标轴建立直角坐标系,若E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交OD于F点.若OF=1,FD=2,则G点的坐标为( )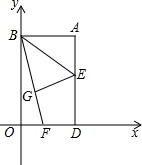 A、( , ) B、( , ) C、( , ) D、( , )10. 如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE= ,BC= .动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
A、( , ) B、( , ) C、( , ) D、( , )10. 如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE= ,BC= .动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )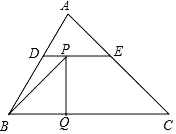 A、
A、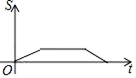 B、
B、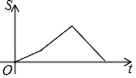 C、
C、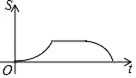 D、
D、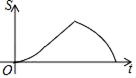
二、填空题
-
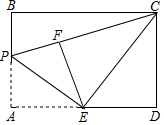
11. =.12. 将抛物线y=﹣5x2先向左平移5个单位.再向下平移3个单位,可以得到新的抛物线是:13. 从﹣2,﹣1,2这三个数中任取两个不同的数相乘,积为正数的概率是.14. 如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为.
三、解答题
-
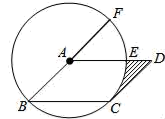
15. 如图,在▱ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙O相交于点F.若 的长为 ,则图中阴影部分的面积为.
 16. 先化简再求值(a+2b)(a﹣2b)﹣(a﹣b)2+5b(a+b).其中a=2﹣ ,b=2+ .17. 某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.
16. 先化简再求值(a+2b)(a﹣2b)﹣(a﹣b)2+5b(a+b).其中a=2﹣ ,b=2+ .17. 某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:
 (1)、本次调查的学生有多少人?(2)、补全上面的条形统计图;(3)、扇形统计图中C对应的中心角度数是;(4)、若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?18. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)、本次调查的学生有多少人?(2)、补全上面的条形统计图;(3)、扇形统计图中C对应的中心角度数是;(4)、若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?18. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P. (1)、求证:PD是⊙O的切线;(2)、求证:AB•CP=BD•CD;(3)、当AB=5cm,AC=12cm时,求线段PC的长.19. 某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度,在河的北岸边点A处,测得河的南岸边点B处在其南偏东45°方向,然后向北走20米到达点C处,测得点B在点C的南偏东33°方向,求出这段河的宽度.(结果精确到1米,参考数据:sin33°=0.54,cos33°≈0.84,tan33°=0.65, ≈1.41)
(1)、求证:PD是⊙O的切线;(2)、求证:AB•CP=BD•CD;(3)、当AB=5cm,AC=12cm时,求线段PC的长.19. 某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度,在河的北岸边点A处,测得河的南岸边点B处在其南偏东45°方向,然后向北走20米到达点C处,测得点B在点C的南偏东33°方向,求出这段河的宽度.(结果精确到1米,参考数据:sin33°=0.54,cos33°≈0.84,tan33°=0.65, ≈1.41)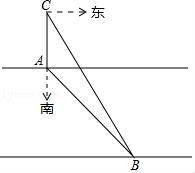 20. 如图,校园有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你用尺规作出灯柱的位置点P.(请保留作图痕迹)
20. 如图,校园有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你用尺规作出灯柱的位置点P.(请保留作图痕迹)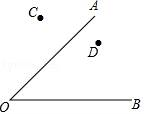 21. 小王是“新星厂”的一名工人,请你阅读下列信息:
21. 小王是“新星厂”的一名工人,请你阅读下列信息:信息一:工人工作时间:每天上午8:00﹣12:00,下午14:00﹣18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲产品数(件)
生产乙产品数(件)
所用时间(分钟)
10
10
350
30
20
850
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元.
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元,请根据以上信息,解答下列问题:
(1)、小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟;(2)、2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?22. 有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90o后得到矩形AMEF(如图1),连接BD,MF,若BD=16cm,∠ADB=30o.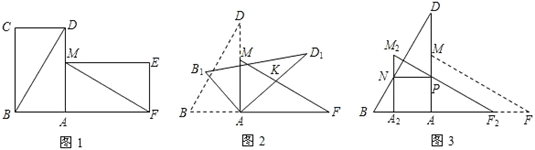 (1)、试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;(2)、把△BCD 与△MEF 剪去,将△ABD绕点A顺时针旋转得△AB1D1 , 边AD1交FM 于点K(如图2),设旋转角为β(0o<β<90o),当△AFK 为等腰三角形时,求β的度数;(3)、若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.23. 抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)、试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;(2)、把△BCD 与△MEF 剪去,将△ABD绕点A顺时针旋转得△AB1D1 , 边AD1交FM 于点K(如图2),设旋转角为β(0o<β<90o),当△AFK 为等腰三角形时,求β的度数;(3)、若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.23. 抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3). (1)、求抛物线的解析式;(2)、如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;(3)、如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(1)、求抛物线的解析式;(2)、如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;(3)、如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.