广西河池市重点中学2019届九年级下学期数学中考一模试卷
试卷更新日期:2019-07-22 类型:中考模拟
一、单选题
-
1. 2019的倒数是( )A、2019 B、﹣2019 C、 D、﹣2. 下列各图中,∠1与∠2互为余角的是( )A、
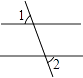 B、
B、 C、
C、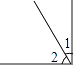 D、
D、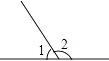 3. 在平面直角坐标系中,点P(2,-3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,该几何体的主视图是( )
3. 在平面直角坐标系中,点P(2,-3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,该几何体的主视图是( )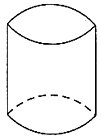 A、
A、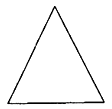 B、
B、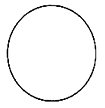 C、
C、 D、
D、 5. 河池市总面积为33500平方公里,其中数据33500用科学记数法表示为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 下列图形中具有稳定性的是( )A、正三角形 B、正方形 C、正五边形 D、正六边形8. 一组数据:5,7,10,5,7,5,6.这组数据的中位数和众数( )A、7和10 B、7和5 C、7和6 D、6和59. 两三角形的相似比是 ,则面积之比是( )A、 B、 C、 D、10. 反比例函数 必经过的点是( )A、 B、 C、 D、11. 若分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±112. 如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB= ,BD=5,则AH的长为( )
5. 河池市总面积为33500平方公里,其中数据33500用科学记数法表示为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 下列图形中具有稳定性的是( )A、正三角形 B、正方形 C、正五边形 D、正六边形8. 一组数据:5,7,10,5,7,5,6.这组数据的中位数和众数( )A、7和10 B、7和5 C、7和6 D、6和59. 两三角形的相似比是 ,则面积之比是( )A、 B、 C、 D、10. 反比例函数 必经过的点是( )A、 B、 C、 D、11. 若分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±112. 如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB= ,BD=5,则AH的长为( )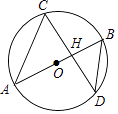 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
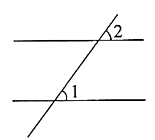
13. .14. 如图,a∥b,∠1=70°,则∠2=.
 15. 方程 的根是.16. 如图,平行四边形 的对角线 、 相交于点 , , , ,则 的周长为.
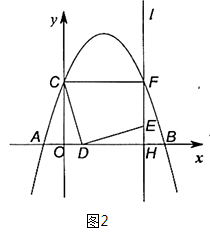
15. 方程 的根是.16. 如图,平行四边形 的对角线 、 相交于点 , , , ,则 的周长为.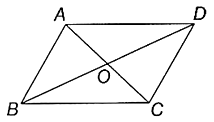 17. 从长为3,5,7,10的四条线段中任意选取三条作为边,能构成三角形的概率是.18. 抛物线 的部分图象如图所示,与 轴的一个交点坐标为 ,抛物线的对称轴是直线 ,下列结论:① ;② ;③方程 有两个不相等的实数根;④抛物线与 轴的另一个交点坐标为 ,其中正确的结论有.
17. 从长为3,5,7,10的四条线段中任意选取三条作为边,能构成三角形的概率是.18. 抛物线 的部分图象如图所示,与 轴的一个交点坐标为 ,抛物线的对称轴是直线 ,下列结论:① ;② ;③方程 有两个不相等的实数根;④抛物线与 轴的另一个交点坐标为 ,其中正确的结论有.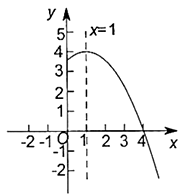
三、解答题
-
19. 计算: .20. 解不等式 ,并把它的解集在数轴上表示出来.21. 如图,在平面直角坐标系中, 三个顶点的坐标分别为 , , .
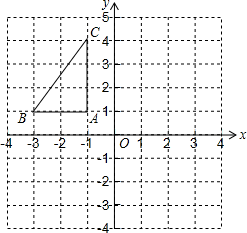 (1)、画出 关于 轴对称的 ;(2)、将 绕点 顺时针旋转90°后得到 ,并求出线段 在旋转过程中所扫过的面积.(结果保留 )22. 我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班,对征集到的作品的数量进行了解析统计,制作了如下两幅不完整的统计图.
(1)、画出 关于 轴对称的 ;(2)、将 绕点 顺时针旋转90°后得到 ,并求出线段 在旋转过程中所扫过的面积.(结果保留 )22. 我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班,对征集到的作品的数量进行了解析统计,制作了如下两幅不完整的统计图.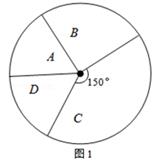
 (1)、李老师采取的调查方式是(填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共件,其中B班征集到作品 , 请把图2补充完整.(2)、如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要在抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出解析过程)23. 如图,在菱形 中,对角线 与 交于点 ,过点 作 的平行线,过点 作 的平行线,两直线相交于点 .
(1)、李老师采取的调查方式是(填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共件,其中B班征集到作品 , 请把图2补充完整.(2)、如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要在抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出解析过程)23. 如图,在菱形 中,对角线 与 交于点 ,过点 作 的平行线,过点 作 的平行线,两直线相交于点 .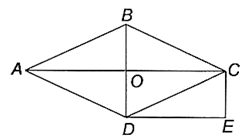 (1)、求证:四边形 是矩形;(2)、若 , ,求菱形 的面积.24. 现有 , 两种商品,买6件 商品和3件 商品用了108元,买5件 商品和1件 商品用了84元.(1)、求 , 两种商品每件多少元?(2)、如果小静准备购买 、 两种商品共10件,总费用不超过120元,且不低于100元,问有几种购买方案?哪种方案费用最低?
(1)、求证:四边形 是矩形;(2)、若 , ,求菱形 的面积.24. 现有 , 两种商品,买6件 商品和3件 商品用了108元,买5件 商品和1件 商品用了84元.(1)、求 , 两种商品每件多少元?(2)、如果小静准备购买 、 两种商品共10件,总费用不超过120元,且不低于100元,问有几种购买方案?哪种方案费用最低?