广西河池市凤山县2019届数学中考一模试卷
试卷更新日期:2019-07-22 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、2 B、 C、 D、2. 计算 的结果是( )A、3 B、2 C、 D、63. 下列运算正确的是( )A、a5﹣a3=a2 B、a6÷a2=a3 C、(﹣2a)3=﹣8a3 D、2a﹣2=4. 如图是由五个相同的小正方块搭成的几何体,其左视图是( )
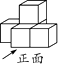 A、
A、 B、
B、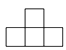 C、
C、 D、
D、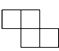 5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 含30°角的直角三角板与直线l1、l2的位置关系如图所示,已知l1∥l2 , ∠ACD=∠A,则∠1=( )
6. 含30°角的直角三角板与直线l1、l2的位置关系如图所示,已知l1∥l2 , ∠ACD=∠A,则∠1=( ) A、70° B、60° C、40° D、30°7. 如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )
A、70° B、60° C、40° D、30°7. 如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( ) A、 B、 C、 D、28. 据统计,某省2015年的贫困人口约382万,截止2017年底,全省贫困人口约190万,设这两年全省贫困人口的年平均下降率为x,则下列方程正确的是( )A、382(1﹣2x)=190 B、382x2=190 C、382(1﹣x)2=190 D、382(1﹣x)+382(1﹣x)2=1909. 小张同学制作了四张材质和外观完全一样的书签,每个书签上写着一本书的名称或一个作者姓名,分别是:《西游记》、施耐庵、《安徒生童话》、安徒生,从这四张书签中随机抽取两张,则抽到的书签正好是相对应的书名和作者姓名的概率是( )A、 B、 C、 D、10. 如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4cm,以点C为圆心,以2cm的长为半径作圆,则⊙C与AB的位置关系是( )
A、 B、 C、 D、28. 据统计,某省2015年的贫困人口约382万,截止2017年底,全省贫困人口约190万,设这两年全省贫困人口的年平均下降率为x,则下列方程正确的是( )A、382(1﹣2x)=190 B、382x2=190 C、382(1﹣x)2=190 D、382(1﹣x)+382(1﹣x)2=1909. 小张同学制作了四张材质和外观完全一样的书签,每个书签上写着一本书的名称或一个作者姓名,分别是:《西游记》、施耐庵、《安徒生童话》、安徒生,从这四张书签中随机抽取两张,则抽到的书签正好是相对应的书名和作者姓名的概率是( )A、 B、 C、 D、10. 如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4cm,以点C为圆心,以2cm的长为半径作圆,则⊙C与AB的位置关系是( )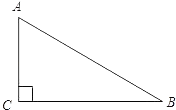 A、相离 B、相切 C、相交 D、相切或相交11. 如图,把抛物线y=x2沿直线y=x平移2 个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
A、相离 B、相切 C、相交 D、相切或相交11. 如图,把抛物线y=x2沿直线y=x平移2 个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )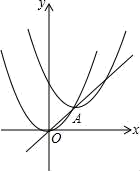 A、y=(x+2)2﹣2 B、y=(x+2)2+2 C、y=(x﹣2)2+2 D、y=(x﹣2)2﹣212. 如图,△ABC中,AB=AC=2,BC=2 ,D点是△ABC所在平面上的一个动点,且∠BDC=60°,则△DBC面积的最大值是( )
A、y=(x+2)2﹣2 B、y=(x+2)2+2 C、y=(x﹣2)2+2 D、y=(x﹣2)2﹣212. 如图,△ABC中,AB=AC=2,BC=2 ,D点是△ABC所在平面上的一个动点,且∠BDC=60°,则△DBC面积的最大值是( ) A、3 B、3 C、 D、2
A、3 B、3 C、 D、2二、填空题
-
13. 将数0.0000078用科学记数法表示为.14. 当x=时,分式 的值为0.15. 平面直角坐标系中,点P(﹣2,4)关于x轴对称的点的坐标为.16. 若正六边形的边长为2,则此正六边形的边心距为 .17. 如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=3,BC=4,则EF的长为.

三、解答题
-
18. 计算:|﹣1|﹣2sin45°+ ﹣2018019. 解不等式组: .20. 如图,延长▱ABCD的边AD到F,使DF=DC,延长CB到点E,使BE=BA,分别连结点A、E和C、F.求证:AE=CF.
 21. 如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.
21. 如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离. 22. 为了解市民对全市创文工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
22. 为了解市民对全市创文工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.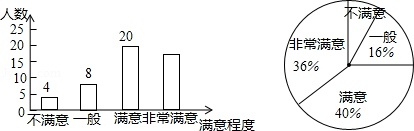
请结合图中信息,解决下列问题:
(1)、求此次调查中接受调查的人数.(2)、求此次调查中结果为非常满意的人数.(3)、兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.23. 某新建成学校举行美化绿化校园活动,九年级计划购买A,B两种花木共100棵绿化操场,其中A花木每棵50元,B花木每棵100元.(1)、若购进A,B两种花木刚好用去8000元,则购买了A,B两种花木各多少棵?(2)、如果购买B花木的数量不少于A花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用.24. 如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD. (1)、试判断PD与⊙O的位置关系,并说明理由;(2)、若点C是弧AB的中点,已知AB=4,求CE•CP的值.25. 如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)、试判断PD与⊙O的位置关系,并说明理由;(2)、若点C是弧AB的中点,已知AB=4,求CE•CP的值.25. 如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.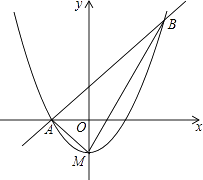 (1)、求抛物线的函数关系式;(2)、判断△ABM的形状,并说明理由;(3)、把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点
(1)、求抛物线的函数关系式;(2)、判断△ABM的形状,并说明理由;(3)、把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点