甘肃省张掖市高台县2019届数学中考模拟试卷（3月）

试卷更新日期：2019-07-22 类型：中考模拟

进入出卷网下载

一、单选题

1. 若a＝（﹣2）^﹣² ， b＝（﹣2）⁰ ， c＝（﹣ $\frac{1}{2}$ ）^﹣¹ ，则a、b、c大小关系是（）

A、a＞c＞b B、b＞a＞c C、a＞b＞c D、c＞a＞b

查看试题解析
2. 下列图形中，是轴对称图形但不是中心对称图形的是（）

A、等边三角形 B、正六边形 C、正方形 D、圆

查看试题解析
3. 将一副三角板（∠A＝30°）按如图所示方式摆放，使得AB∥EF，则∠1等于（）

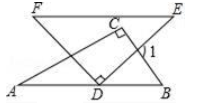A、75° B、90° C、105° D、115°

查看试题解析
4. 下列计算正确的是（）

A、3a﹣a＝2 B、a²+a³＝a⁵ C、a⁶÷a²＝a⁴ D、（a²）³＝a⁵

查看试题解析
5. 关于 $x$ 的一元二次方程 $x^{2} - (k + 3) x + k = 0$ 的根的情况是（）

A、有两不相等实数根 B、有两相等实数根 C、无实数根 D、不能确定

查看试题解析
6. 关于反比例函数y= $\frac{2}{x}$ ，下列说法中错误的是（）

A、它的图象是双曲线 B、它的图象在第一、三象限 C、y的值随x的值增大而减小 D、若点（a，b）在它的图象上，则点（b，a）也在它的图象上

查看试题解析
7. 已知⊙O的直径CD=10cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB=8cm，则AC的长为( )

A、 $2 \sqrt{5}$ cm B、 $4 \sqrt{5}$ cm C、 $2 \sqrt{5}$ cm或 $4 \sqrt{5}$ cm D、 $2 \sqrt{3}$ cm或 $4 \sqrt{3}$ cm

查看试题解析
8. 已知：菱形ABCD中，对角线AC与BD相交于点O，OE∥DC交BC于点E，AD=6cm，则OE的长为（）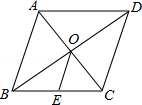

A、6cm B、4cm C、3cm D、2cm

查看试题解析
9. 如图，直线y＝﹣x﹣1与y＝kx+b（k≠0且k，b为常数）的交点坐标为（﹣2，l），则关于x的不等式﹣x﹣1＜kx+b的解集为（）

A、x＞﹣2 B、x＜﹣2 C、x＞1 D、x＜l

查看试题解析
10. A，B两地相距90km，甲骑摩托车由A地出发，去B地办事，甲出发的同时，乙骑自行车同时由B地出发沿着同一条道路前往A地，甲办完事后原速返回A地，结果比乙早到0.5小时.甲、乙两人离A地距离y（km）与时间x（h）的函数关系图像如图所示.下列说法：①.a=3.5，b=4；② 甲走的全路程是90km；③乙的平均速度是22.5km/h；.④甲在B地办事停留了0.5小时.其中正确的说法有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 要使分式 $\frac{2}{1 - x}$ 有意义，则 $x$ 应满足的条件是．

查看试题解析
12. 把多项式mx²﹣4my²分解因式的结果是.

查看试题解析
13. 已知菱形的周长为40cm，两个相邻角度数比为1：2，则较短的对角线长为，面积为.

查看试题解析
14. 如图，⊙O的直径CD⊥弦AB，垂足为E，∠AOE＝50°，则∠BCD等于.

查看试题解析
15. 甲、乙两地相距160km，一辆长途汽车从甲地开出3小时后，一辆小轿车也从甲地开出，结果小轿车与长途汽车同时到达乙地.已知小轿车的速度是长途汽车的3倍，设长途汽车的速度为x千米/时，则小轿车的速度为3x千米/时，依题意可列方程为.

查看试题解析
16. 二次函数y=x²＋2x－3与x轴两交点之间的距离为.

查看试题解析
17. 已知A（m，3）、B（﹣2，n）在同一个反比例函数图象上，则 $\frac{m}{n}$ ＝.

查看试题解析
18. 一组按规律排列的式子： $\frac{2}{a}$ ， $\frac{5}{a^{2}}$ ， $\frac{10}{a^{3}}$ ， $\frac{17}{a^{4}}$ ， $\frac{26}{a^{5}}$ ，…，其中第7个式子是，第 $n$ 个式子是（用含的 $n$ 式子表示， $n$ 为正整数）.

查看试题解析

三、解答题

19. 计算 $\sqrt{2}$ sin45°+3tan30°﹣（π﹣1）⁰

查看试题解析
20. 如图

(1)、请画出△ABC关于直线l的轴对称图形△A₁B₁C₁.

(2)、将△ABC绕着点B旋转180°得到△A₂B₂C₂ ，并画出图形.（保留作图痕迹，不写画法，注明结论）

查看试题解析
21. 如图，飞机沿水平线AC飞行，在A处测得正前方停泊在海面上某船只P的俯角∠CAP（从高处观测低处的目标时，视线与水平线所成的锐角）为15°，飞行10km到达B处，在B处测得该船只的俯角∠CBP＝52°，求飞机飞行的高度（精确到1m）

查看试题解析
22. 不透明的袋子中装有4个相同的小球，它们除颜色外无其它差别，把它们分别标号：1、2、3、4

(1)、随机摸出一个小球后，放回并摇匀，再随机摸出一个，用列表或画树状图的方法求出“两次取的球标号相同”的概率

(2)、随机摸出两个小球，直接写出“两次取出的球标号和等于4”的概率.

查看试题解析
23. 我省有关部门要求各中小学要把“阳光体育”写入课表，为了响应这一号召，某校围绕着“你最喜欢的体育活动项目是什么？(只写一项)”的问题，对在校学生进行了随机抽样调查，从而得到一组数据，如图1是根据这组数据绘制的条形统计图，请结合统计图回答下列问题：

(1)、该校对多少名学生进行了抽样调查？

(2)、本次抽样调查中，最喜欢足球活动的有多少人？占被调查人数的百分比是多少？

(3)、若该校九年级共有400名学生，图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图，请你估计全校学生中最喜欢篮球活动的人数约为多少？

查看试题解析
24. 如图，已知 $A (n ， - 2) ， B (1 ， 4)$ 是一次函数 $y = k x + b$ 的图象和反比例函数 $y = \frac{m}{x}$ 的图象的两个交点，直线AB与y轴交于点C.

(1)、求反比例函数和一次函数的关系式；

(2)、求△AOC的面积.

查看试题解析
25. 如图，菱形ABCD中， $BC = \sqrt{6}$ ， $∠ C = 135^{\circ}$ ，以点A为圆心的 $⊙ A$ 与BC相切于点E.

(1)、求证：CD是 $⊙ A$ 的切线；

(2)、求图中阴影部分的面积.

查看试题解析
26. 甲商品的进价为每件20元，商场将其售价从原来的每件40元进行两次调价，已知该商品现价为每件32.4元.

(1)、若该商品两次调价的降价率相同，求这个降价率；

(2)、经调查，该商品每降价0.2元，即可多销售10件. 已知甲商品售价40元时每月可销售500件，若该商场希望该商品每月能盈利10000元，且尽可能扩大销售量，则该商品在现价的基础上还应如何调整？

查看试题解析
27. 如图，在平行四边形ABCD中，AB＝6，BC＝10，对角线AC⊥AB，点E、F分别是BC、AD上的点，且BE＝DF.

(1)、求证：四边形AECF是平行四边形；

(2)、当BE长度为时，四边形AECF是菱形.

查看试题解析
28. 如图1，抛物线y=ax²+bx+3交x轴于点A（﹣1，0）和点B（3，0）．

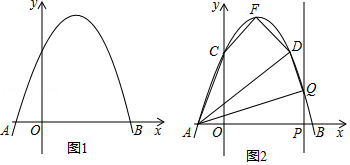(1)、求该抛物线所对应的函数解析式；

(2)、如图2，该抛物线与y轴交于点C，顶点为F，点D（2，3）在该抛物线上．
①求四边形ACFD的面积；

②点P是线段AB上的动点（点P不与点A、B重合），过点P作PQ⊥x轴交该抛物线于点Q，连接AQ、DQ，当△AQD是直角三角形时，求出所有满足条件的点Q的坐标．

查看试题解析