江苏省张家港市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-07-22 类型:期末考试
一、单选题
-
1. 下列调查中,适合采用普查的是( )A、夏季冷饮市场上冰激凌的质量 B、某本书中的印刷错误 C、《舌尖上的中国》第三季的收视率 D、公民保护环境的意识2. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、3. 一元二次方程 配方后可变形为( )A、 B、 C、 D、4. 一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为( )
 A、 B、 C、 D、5. 如图,在 中,已知 , 分别为边 , 的中点,连结 ,若 ,则 等于( )
A、 B、 C、 D、5. 如图,在 中,已知 , 分别为边 , 的中点,连结 ,若 ,则 等于( )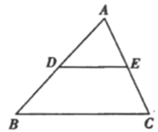 A、70º B、67. 5º C、65º D、60º6. 下列说法正确的是( )A、某日最低气温是–2℃,最高气温是4℃,则该日气温的极差是2℃ B、一组数据2,2,3,4,5,5,5,这组数据的众数是2 C、小丽的三次考试的成绩是116分,120分,126分,则小丽这三次考试平均数是121分 D、一组数据2,2,3,4,这组数据的中位数是2.57. 如图,在平行四边形 中, , 是对角线 上不同的两点,连接 , , , .下列条件中,不能得出四边形 一定是平行四边形的为( )
A、70º B、67. 5º C、65º D、60º6. 下列说法正确的是( )A、某日最低气温是–2℃,最高气温是4℃,则该日气温的极差是2℃ B、一组数据2,2,3,4,5,5,5,这组数据的众数是2 C、小丽的三次考试的成绩是116分,120分,126分,则小丽这三次考试平均数是121分 D、一组数据2,2,3,4,这组数据的中位数是2.57. 如图,在平行四边形 中, , 是对角线 上不同的两点,连接 , , , .下列条件中,不能得出四边形 一定是平行四边形的为( )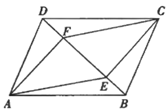 A、 B、 C、 D、8. 计算 的结果是( )A、 B、 C、 D、9. 如图,已知一次函数 的图像与 轴, 轴分别交于 , 两点,与反比例函数 在第一象限内的图像交于点 ,且 为 的中点,则一次函数的解析式为( )
A、 B、 C、 D、8. 计算 的结果是( )A、 B、 C、 D、9. 如图,已知一次函数 的图像与 轴, 轴分别交于 , 两点,与反比例函数 在第一象限内的图像交于点 ,且 为 的中点,则一次函数的解析式为( )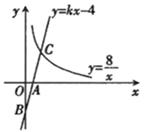 A、 B、 C、 D、10. 如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是( )
A、 B、 C、 D、10. 如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是( )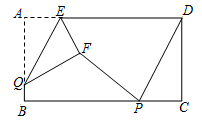 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
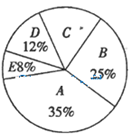
11. 若式子 有意义,则实数 的取值范围是.12. 当 时,分式 的值为0.13. 某中学组织八年级学生进行“绿色出行,低碳生活”知识竞赛,为了了解本次竞赛的成绩,把学生成绩分成 五个等级,并绘制如图所示的扇形统计图(不完整)统计成绩,则 等级所在扇形的圆心角是.
 14. 矩形 的对角线 与 相交于点 , , , 分别是 , 的中点,则 的长度为.
14. 矩形 的对角线 与 相交于点 , , , 分别是 , 的中点,则 的长度为. 15. 已知关于 的一元二次方程 的两个实数根分别是x =-2,x =4,则 的值为.16. 如图,将矩形 沿 折叠,使点 落在 边上的点 处,点 落在点 处,已知 ,连接 ,则 .
15. 已知关于 的一元二次方程 的两个实数根分别是x =-2,x =4,则 的值为.16. 如图,将矩形 沿 折叠,使点 落在 边上的点 处,点 落在点 处,已知 ,连接 ,则 .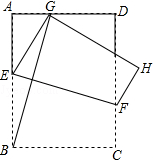 17. 如图,点A是反比例函数y = (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y = (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为.
17. 如图,点A是反比例函数y = (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y = (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为.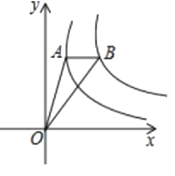 18. 如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm )随时间x(s)变化的关系图象,则a的值是
18. 如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm )随时间x(s)变化的关系图象,则a的值是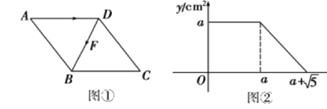
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 解下列方程:(1)、 ;(2)、 .21. 如图,已知正比例函数y =ax的图象与反比例函数 的图象有一个公共点A(1,2).
 (1)、求这两个函数表达式;(2)、根据图象写出正比例函数值大于反比例函数值的x的取值范围;(3)、根据反比例函数的图象,写出当−2<x<−1时y 的取值范围。22. 如图,四边形 是菱形,对角线 , 相交于点 ,且 .
(1)、求这两个函数表达式;(2)、根据图象写出正比例函数值大于反比例函数值的x的取值范围;(3)、根据反比例函数的图象,写出当−2<x<−1时y 的取值范围。22. 如图,四边形 是菱形,对角线 , 相交于点 ,且 .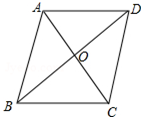 (1)、求菱形 的周长;(2)、若 ,求 的长.23. 某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.
(1)、求菱形 的周长;(2)、若 ,求 的长.23. 某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.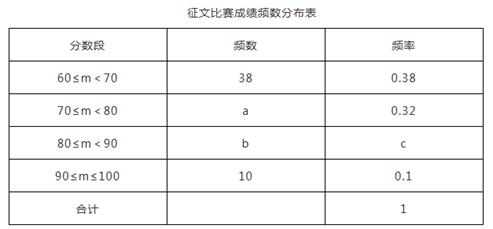
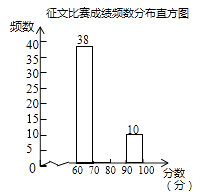
请根据以上信息,解决下列问题:
(1)、征文比赛成绩频数分布表中c的值是;(2)、补全征文比赛成绩频数分布直方图;(3)、若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.24. 有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).(1)、请用表格或树状图列出点A所有可能的坐标;(2)、求点A在反比例函数y= 图象上的概率.25. 某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.(1)、填表:(不需化简)时间
第一个月
第二个月
清仓时
单价(元)
80
40
销售量(件)
200
(2)、如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?26. 如图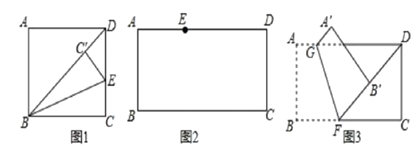 (1)、如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C'处,若∠ADB=46°,则∠DBE的度数为∘.(2)、小明手中有一张矩形纸片ABCD,AB=4,AD=9.
(1)、如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C'处,若∠ADB=46°,则∠DBE的度数为∘.(2)、小明手中有一张矩形纸片ABCD,AB=4,AD=9.【画一画】
如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
【算一算】
如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A',B'处,若AG= ,求B'D的长;
27. 已知:如图,在正方形ABCD外取−点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,已知AE=AP=BE=1.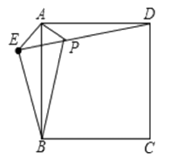 (1)、求证:△APD≌△AEB;(2)、连接PC,求线段PC的长度;(3)、试求正方形ABCD的面积。28. 如图,矩形OABC的顶点A.C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y= (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3, ).
(1)、求证:△APD≌△AEB;(2)、连接PC,求线段PC的长度;(3)、试求正方形ABCD的面积。28. 如图,矩形OABC的顶点A.C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y= (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3, ).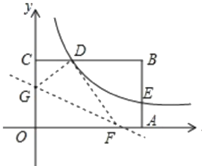 (1)、求反比例函数的表达式和m的值;(2)、将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式。
(1)、求反比例函数的表达式和m的值;(2)、将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式。