河南省漯河市郾城区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-07-22 类型:期末考试
一、单选题
-
1. 下列各式中,最简二次根式是( )A、 B、 C、 D、2. 已知一次函数 ,若 随 的增大而增大,则 的取值范围是( )A、 B、 C、 D、3. 如图,菱形ABCD的对角线AC=5,BD=10,则该菱形的面积为( )
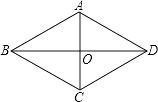 A、50 B、25 C、 D、12.54. 甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
A、50 B、25 C、 D、12.54. 甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:选手
甲
乙
丙
丁
平均数(环)
9.2
9.2
9.2
9.2
方差(环2)
0.035
0.015
0.025
0.027
则这四人中成绩发挥最稳定的是( )
A、甲 B、乙 C、丙 D、丁5. 估计 的值在下列哪两个整数之间( )A、6和7之间 B、7和8之间 C、8和9之间 D、无法确定6. 一组数据为:31 30 35 29 30,则这组数据的方差是( )A、22 B、18 C、3.6 D、4.47. 如图,在边长为1的正方形组成的网格图中标有 、 、 、 四条线段,其中能构成一个直角三角形三边的线段是( ) A、 , , B、 , , C、 , , D、 , ,8. 关于 的一次函数
A、 , , B、 , , C、 , , D、 , ,8. 关于 的一次函数 的图象可能正确的是( ) A、
的图象可能正确的是( ) A、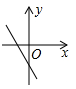 B、
B、 C、
C、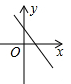 D、
D、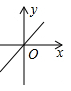 9. 下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,照此规律排列下去,则第8个图中小正方形的个数是( )
9. 下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,照此规律排列下去,则第8个图中小正方形的个数是( ) A、48 B、63 C、80 D、9910. 如图1,将正方形 置于平面直角坐标系中,其中 边在 轴上,其余各边均与坐标轴平行.直线 沿 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形 的边所截得的线段长为 ,平移的时间为 (秒), 与 的函数图象如图2所示,则图2中 的值为( )
A、48 B、63 C、80 D、9910. 如图1,将正方形 置于平面直角坐标系中,其中 边在 轴上,其余各边均与坐标轴平行.直线 沿 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形 的边所截得的线段长为 ,平移的时间为 (秒), 与 的函数图象如图2所示,则图2中 的值为( )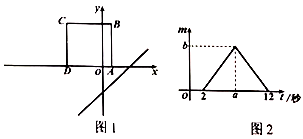 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知直线 与 轴交于点 ,则关于 的方程 的解为 .12. 如 图,在 中,已知 , , DE 平分 交 边于点 ,则 等于 .
 13. 某市某活动中心组织了一次少年跳绳比赛,各年龄组的参赛人数如表所示:
13. 某市某活动中心组织了一次少年跳绳比赛,各年龄组的参赛人数如表所示:年龄组
12岁
13岁
14岁
15岁
参赛人数
5
19
13
13
则全体参赛选手年龄的中位数是.
14. 设 的整数部分为 ,小数部分为 ,则 的值等于.15. 如图,正方形 的边长为6,点 是 上的一点,连接 并延长交射线 于点 ,将 沿直线 翻折,点 落在点 处, 的延长线交 于点 ,当 时,则 的长为.
三、解答题
-
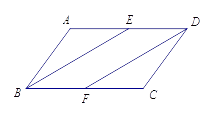
16. 如图,在 中,点 , 分别在边 , 上, ,求证: .
 17. 计算:(1)、(2)、18. 某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
17. 计算:(1)、(2)、18. 某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.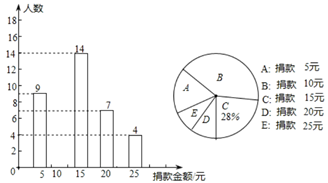 (1)、本次共抽查学生多少人?并将条形统计图补充完整;(2)、请直接写出捐款金额的众数和中位数,并计算捐款的平均数;(3)、在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?19. 如图,直线 的解析式为 ,与 交于点 ,直线 经过点 ,与直线 交于点 ,且与 轴交于点 .
(1)、本次共抽查学生多少人?并将条形统计图补充完整;(2)、请直接写出捐款金额的众数和中位数,并计算捐款的平均数;(3)、在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?19. 如图,直线 的解析式为 ,与 交于点 ,直线 经过点 ,与直线 交于点 ,且与 轴交于点 . (1)、求点 的坐标及直线 及的解析式;(2)、求 的面积.20. 小明和小亮两人从甲地出发,沿相同的线路跑向乙地,小明先跑一段路程后,小亮开始出发,当小亮超过小明150米时,小亮停在此地等候小明,两人相遇后,小亮和小明一起以小明原来的速度跑向乙地,如图是小明、小亮两人在跑步的全过程中经过的路程 (米)与小明出发的时间 (秒)的函数图象,请根据题意解答下列问题.
(1)、求点 的坐标及直线 及的解析式;(2)、求 的面积.20. 小明和小亮两人从甲地出发,沿相同的线路跑向乙地,小明先跑一段路程后,小亮开始出发,当小亮超过小明150米时,小亮停在此地等候小明,两人相遇后,小亮和小明一起以小明原来的速度跑向乙地,如图是小明、小亮两人在跑步的全过程中经过的路程 (米)与小明出发的时间 (秒)的函数图象,请根据题意解答下列问题.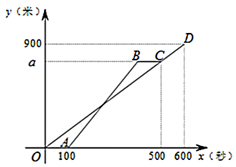 (1)、在跑步的全过程中,小明共跑了米,小明的速度为米/秒;(2)、求小亮跑步的速度及小亮在途中等候小明的时间;(3)、求小亮出发多长时间第一次与小明相遇?21. 如图,在菱形 中, ,过点 作 于点 ,交对角线 于点 ,过点 作 于点 .
(1)、在跑步的全过程中,小明共跑了米,小明的速度为米/秒;(2)、求小亮跑步的速度及小亮在途中等候小明的时间;(3)、求小亮出发多长时间第一次与小明相遇?21. 如图,在菱形 中, ,过点 作 于点 ,交对角线 于点 ,过点 作 于点 .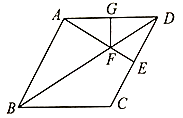 (1)、若 ,求四边形 的面积;(2)、求证: .(温馨提示;连接 )22. 某厨具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如下表:
(1)、若 ,求四边形 的面积;(2)、求证: .(温馨提示;连接 )22. 某厨具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如下表:进价(元/台)
售价(元/台)
电饭煲
200
250
电压锅
160
200
(1)、一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?(2)、为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的 ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?23. 如图,矩形 摆放在平面直角坐标系中,点 在 轴上,点 在 轴上,, ,过点 的直线交矩形 的边 于点 ,且点 不与点 、 重合,过点 作 , 交 轴于点 ,交 轴于点 .
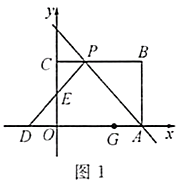
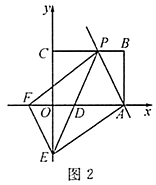 (1)、如图1,若 为等腰直角三角形,求直线 的函数解析式;(2)、如图2,过点 作 交 轴于点 ,若四边形 是平行四边形,求直线 的解析式.
(1)、如图1,若 为等腰直角三角形,求直线 的函数解析式;(2)、如图2,过点 作 交 轴于点 ,若四边形 是平行四边形,求直线 的解析式.