江苏省苏州市高新区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-22 类型:期末考试
一、单选题
-
1. 计算的 结果是( )A、 B、 C、 D、2. 不等式2x+3≥5的解集在数轴上表示正确的是( )
A、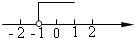 B、
B、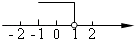 C、
C、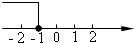 D、
D、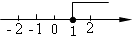 3. 画△ABC中AC边上的高,下列四个画法中正确的是( )A、
3. 画△ABC中AC边上的高,下列四个画法中正确的是( )A、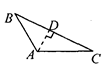 B、
B、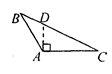 C、
C、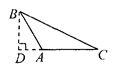 D、
D、 4. 如果 , ,那么 等于( )A、 B、 C、 D、5. 已知 是方程组 的解,则 的值是( )A、–1 B、1 C、2 D、36. 如图,已知 , ,增加下列条件:① ;② ;③ ;④ .其中能使 的条件有( )
4. 如果 , ,那么 等于( )A、 B、 C、 D、5. 已知 是方程组 的解,则 的值是( )A、–1 B、1 C、2 D、36. 如图,已知 , ,增加下列条件:① ;② ;③ ;④ .其中能使 的条件有( )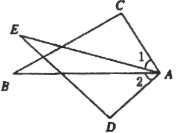 A、4个 B、3个 C、2个 D、1个7. 若 , ,则 、 的大小关系为( )A、 > B、 < C、 = D、无法确定8. 如图,把一长方形纸片沿 折盈后,点 、 分别落在 、 的位置,若 ,则 等于( )
A、4个 B、3个 C、2个 D、1个7. 若 , ,则 、 的大小关系为( )A、 > B、 < C、 = D、无法确定8. 如图,把一长方形纸片沿 折盈后,点 、 分别落在 、 的位置,若 ,则 等于( ) A、65º B、62º C、56º D、64º9. 已知如图, , , 且 , , ,则 的面积为( )
A、65º B、62º C、56º D、64º9. 已知如图, , , 且 , , ,则 的面积为( ) A、1 B、2 C、4 D、无法确定
A、1 B、2 C、4 D、无法确定二、填空题
-
10. 若 , ,则 .11. 如图, 、 两点分别位于一个池塘的两端, 是 的中点,也是 的中点,若DE=20米,则 的长为米.
 12. 如图所示,将含有30°角的三角板的直角顶点放在互相平行的两条直线其中一条上,若∠1=35°,则∠2的度数为度
12. 如图所示,将含有30°角的三角板的直角顶点放在互相平行的两条直线其中一条上,若∠1=35°,则∠2的度数为度 13. 若关于 的不等式 的解集为 ,化简 .14. 若二元一次方程组 的解 , 的值恰好是一个等腰三角形的腰和底边的长,且这个等腰三角形的周长为7,则 的值为.15. 如图,若 和 的面积分别为 、 ,则 .
13. 若关于 的不等式 的解集为 ,化简 .14. 若二元一次方程组 的解 , 的值恰好是一个等腰三角形的腰和底边的长,且这个等腰三角形的周长为7,则 的值为.15. 如图,若 和 的面积分别为 、 ,则 .
三、解答题
-
16. 计算:(1)、 .(2)、 .17. 因式分解:(1)、 .(2)、 .18. 解不等式组 ,并写出该不等式组的最大整数解.19. 先化简,再求值: ,其中
20. 叙述三角形内角和定理并将证明过程填写完整.
定理:.
已知: ,求证: .
证明:作边 的延长线 ,过 点作 .
∴ (直线平行,内错角相等),
(),
∵ (平角定义),
∴ ().
21. 如图, 、 、 三点在同一条直线上, , , .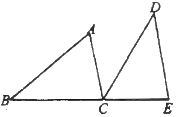 (1)、求证: ;(2)、若 ,求 的度数.22. 已知 , .求下列各式的值:(1)、 .(2)、 .23. 如图,在 中, 的平分线交 于点 , , .
(1)、求证: ;(2)、若 ,求 的度数.22. 已知 , .求下列各式的值:(1)、 .(2)、 .23. 如图,在 中, 的平分线交 于点 , , . (1)、如图1,若 ,垂足为 ,求 的度数;(2)、如图2,若点 是 延长线上的一点, 、 的平分线交于点 ,求 的度数.24. 某商场有A、B两种商品,每件的进价分别为15元、35元.商场销售5件A商品和2件B商品,可获得利润45元;销售8件A商品和4件B商品,可获得利润80元.(1)、求A、B两种商品的销售单价;(2)、如果该商场计划购进A、B两种商品共80件,用于进货资金最多投入2 000元,但又要确保获利至少590元,请问有那几种进货方案?25. 如图,在边长为6cm的正方形ABCD中,动点P从点A出发,沿线段AB以每秒1cm的速度向点B运动;同时动点Q从点B出发,沿线段BC以每秒2cm的速度向点C运动.当点Q到达C点时,点P同时停止,设运动时间为t秒.(注:正方形的四边长都相等,四个角都是直角)
(1)、如图1,若 ,垂足为 ,求 的度数;(2)、如图2,若点 是 延长线上的一点, 、 的平分线交于点 ,求 的度数.24. 某商场有A、B两种商品,每件的进价分别为15元、35元.商场销售5件A商品和2件B商品,可获得利润45元;销售8件A商品和4件B商品,可获得利润80元.(1)、求A、B两种商品的销售单价;(2)、如果该商场计划购进A、B两种商品共80件,用于进货资金最多投入2 000元,但又要确保获利至少590元,请问有那几种进货方案?25. 如图,在边长为6cm的正方形ABCD中,动点P从点A出发,沿线段AB以每秒1cm的速度向点B运动;同时动点Q从点B出发,沿线段BC以每秒2cm的速度向点C运动.当点Q到达C点时,点P同时停止,设运动时间为t秒.(注:正方形的四边长都相等,四个角都是直角) (1)、CQ的长为cm(用含 的代数式表示);(2)、连接DQ并把DQ沿DC翻折,交BC延长线于点F.连接DP、DQ、PQ.
(1)、CQ的长为cm(用含 的代数式表示);(2)、连接DQ并把DQ沿DC翻折,交BC延长线于点F.连接DP、DQ、PQ.①若 ,求t的值.
②当 时,求t的值,并判断 与 是否全等,请说明理由.