湖北省监利县2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2019-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 以下各数中， $\sqrt{5}$ 、﹣2、0、3 $\sqrt{4}$ 、 $\frac{22}{7}$ 、﹣1.732、 $\sqrt{25}$ 、 $\frac{π}{2}$ 、3+ $\sqrt{29}$ 、0.1010010001…中无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列调查方式合适的是（）

A、为了了解市民对电影《战狼》的感受，小华在某校随机采访了8名初三学生 B、为了了解我国中学生对国家“一带一路”的战略的知晓率，小民在网上向3位中学生好友做了调查 C、为了了解“嫦娥一号”卫星零部件的状况，检测人员采用了普查的方式 D、为了了解电视栏目《朗读者》的收视率，统计人员采用了普查的方式

查看试题解析
3. 小亮在解不等式组 ${\begin{matrix} 6 - 2 x < 0 ① \\ x + 5 > - 3 ② \end{matrix}$ 时，解法步骤如下：
解不等式①，得x＞3，…第一步；
解不等式②，得x＞﹣8，…第二步；
所有原不等式组组的解集为﹣8＜x＜3…第三步．
对于以上解答，你认为下列判断正确的是（）

A、解答有误，错在第一步 B、解答有误，错在第二步 C、解答有误，错在第三步 D、原解答正确无误

查看试题解析
4. 下列运算正确的（）

A、(﹣3)²＝﹣9 B、 $\sqrt{{(- 5)}^{2}} = - 5$ C、 $\sqrt{\frac{25}{16}} = \pm \frac{5}{4}$ D、 $\sqrt[3]{- 64} = - 4$

查看试题解析
5. (a，－6)关于x轴的对称点的坐标为（）

A、(－a， 6) B、(a， 6) C、(a，－6) D、(－a，－6)

查看试题解析
6. 如图，下列能判定AB∥CD的条件有（）个.
( 1 )∠B+∠BCD＝180°；(2)∠1＝∠2；(3)∠3＝∠4；(4)∠B＝∠5.

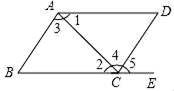A、1 B、2 C、3 D、4

查看试题解析
7.
如图，直线m∥n，将含有45°角的三角板ABC的直角顶点C放在直线n上，则∠1+∠2等于（）

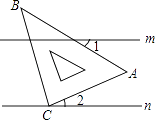A、30° B、40° C、45° D、60°

查看试题解析
8. 甲、乙两人做同样的零件，如果甲先做1天，乙再开始做，5天后两人做的一样多，如果甲先做30个，乙再开始做，4天后乙反比甲多做10个．甲，乙两人每天分别做多少个？设甲，每天做x个，乙每天做y个，列出的方程组是（）

A、 ${\begin{matrix} 6 x = 5 y \\ 30 + 4 x = 4 y + 10 \end{matrix}$ B、 ${\begin{matrix} 1 + 5 x = 6 y \\ 30 + 4 x = 4 y - 10 \end{matrix}$ C、 ${\begin{matrix} 6 x = 5 y \\ 30 + 4 x = 4 y - 10 \end{matrix}$ D、 ${\begin{matrix} 1 + 5 x = 5 y \\ 30 + 4 x = 4 y + 10 \end{matrix}$

查看试题解析
9. 经过点M（4，－2）与点N（x，y）的直线平行于x轴，且点N到y轴的距离等于5，由点N的坐标是（）

A、（5，2）或（－5，－2） B、（5，－2）或（－5，－2） C、（5，－2）或（－5，2） D、（5，－2）或（－2，－2）

查看试题解析
10. 如图是一个运算程序的示意图，若开始输入x的值为81，则第2019次输出的结果为（）

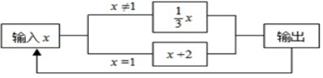A、3 B、27 C、9 D、1

查看试题解析

二、填空题

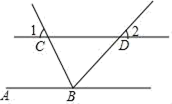
11. 使式子 $\sqrt{3 - 2 m}$ 有意义的m的取值范围是

查看试题解析
12. 已知关于x的方程3a﹣x＝x+2的解为2，则代数式a²+1＝

查看试题解析
13. 已知坐标平面内一动点P(1，2)，先沿x轴的正方向平移3个单位，再沿y轴的负半轴方向平移3个单位后停止，此时P的坐标是

查看试题解析
14. 如图，直线AB∥CD，BC平分∠ABD，∠1＝55°，图中∠2＝

查看试题解析
15. 某公园划船项目收费标准如下：
船型
两人船
（限乘两人）
四人船
（限乘四人）
六人船
（限乘六人）
八人船
（限乘八人）
每船租金
（元/小时）
90
100
130
150
某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为元．

查看试题解析
16. 如果不等式组 ${\begin{array}{l} 3 x - a \geq 0 \\ 2 x - b < 0 \end{array}$ 的整数解仅为2，且a、b均为整数，则代数式2a²+b的最大值＝.

查看试题解析

三、解答题

17. 计算与求解：

(1)、 $\sqrt[3]{- 8} + \sqrt{\frac{9}{25}} - | \sqrt{7} - 3 |$ .

(2)、已知 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 3 \\ b x + a y = - 7 \end{array}$ 的解，求a、b的值.

查看试题解析
18.

(1)、解不等式组解不等式组 ${\begin{cases} \frac{- 2 x - 3}{2} + 1 < 0 \\ 2 + \frac{7 - x}{4} > x \end{cases}$ ，并把解集在数轴上标出来.

(2)、解不等式组 ${\begin{cases} 3 (x - 3) < x - 1 ① \\ x - \frac{5 - x}{3} \geq \frac{1}{2} ② \end{cases}$ ，并写出它的所有整数解.

查看试题解析
19. 如图，是一块破损的木板.

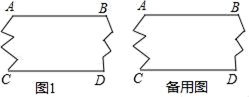
(1)、请你设计一种方案，检验木板的两条直线边缘AB、CD是否平行；

(2)、若AB∥CD，连接BC，过点A作AM⊥BC于M，垂足为M，画出图形，并写出∠BCD与∠BAM的数量关系.

查看试题解析
20. 某市为提倡节约用水，准备实行自来水阶梯计算方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行加价收费，为了更好地决策，自来水公司随机抽取了部分用户的用水量数据，并绘制了如图不完整的统计图，（每组数据包括在右端点但不包括左端点），请你根据统计图解答下列问题：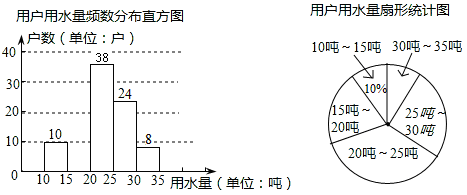

(1)、此次抽样调查的样本容量是

(2)、补全频数分布直方图，求扇形图中“15吨～20吨”部分的圆心角的度数.

(3)、如果自来水公司将基本用水量定为每户25吨，那么该地区10万用户中约有多少用户的用水全部享受基本价格？

查看试题解析
21. 如图，在三角形ABC中，过A作AD⊥BC，垂足为D，E为AB上一点，过点E作EF⊥BC，垂足为点F，过点D作DG∥AB交AC于点G.

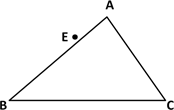(1)、依题意补全图形；

(2)、求证：∠BEF＝∠ADG

查看试题解析
22. 阅读材料：善于思考的小明在解方程组 ${\begin{cases} 4 x + 10 y = 6 ① \\ 8 x + 22 y = 10 ② \end{cases}$ 时，采用了一种“整体代换”的解法，解法如下：
解：将方程②8x+20y+2y=10，变形为 2（4x+10y）+2y=10③，把方程①代入③得，2×6+2y=10，则 y=﹣1；把 y=﹣1 代入①得，x=4，所以方程组的解为： ${\begin{cases} x = 4 \\ y = - 1 \end{cases}$ 请你解决以下问题：

(1)、试用小明的“整体代换”的方法解方程组 ${\begin{cases} 2 x - 3 y = 7 ① \\ 6 x - 5 y = 11 ② \end{cases}$

(2)、已知 x、y、z，满足 ${\begin{cases} 3 x - 2 z + 12 y = 47 ① \\ 2 x + z + 8 y = 36 ② \end{cases}$ 试求 z 的值.

查看试题解析
23. 如图1，AM∥CN，点B为平面内一点，AB⊥BC于B，过B作BD⊥AM.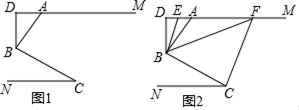

(1)、求证：∠ABD＝∠C；

(2)、如图2，在(1)问的条件下，分别作∠ABD、∠DBC的平分线交DM于E、F，若∠BFC＝1.5∠ABF，∠FCB＝2.5∠BCN，
①求证：∠ABF＝∠AFB；

②求∠CBE的度数.

查看试题解析