河南省卫辉市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-22 类型:期末考试
一、单选题
-
1. 在一些美术字中,有的汉字是轴对称图形,下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 ,则下列一定成立的是( )A、 B、 C、 D、3. 商店将某种商品按进货价提高100%后,又以八折售出,售价为80元,则这种商品的进价是( )A、100元 B、80元 C、60元 D、50元4. 只用下列一种正多边形就能铺满地面的是( )A、正十边形 B、正八边形 C、正六边形 D、正五边形5. 如图,在 中, ,则 的度数为( )
2. 若 ,则下列一定成立的是( )A、 B、 C、 D、3. 商店将某种商品按进货价提高100%后,又以八折售出,售价为80元,则这种商品的进价是( )A、100元 B、80元 C、60元 D、50元4. 只用下列一种正多边形就能铺满地面的是( )A、正十边形 B、正八边形 C、正六边形 D、正五边形5. 如图,在 中, ,则 的度数为( )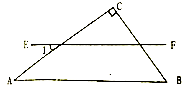 A、 B、 C、 D、6. 若关于 的方程 的解不大于 ,则 的取值范围是( )A、 B、 C、 D、7. 中华文化十大精深,源远流长,我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子短一托。”其大意 为:现有一根竿和一要绳索,折回索子来量竿,却比竿尺;如果将绳索对半折后再去量竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果绳索对半折后再去量竿,就比竿短5尺.设绳索长 尺,竿长 尺,则符合题意的方程组是( )A、 B、 C、 D、8. 已知 是 的三边长,化简 的值是( )A、 B、 C、 D、9. 小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是( )A、
A、 B、 C、 D、6. 若关于 的方程 的解不大于 ,则 的取值范围是( )A、 B、 C、 D、7. 中华文化十大精深,源远流长,我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子短一托。”其大意 为:现有一根竿和一要绳索,折回索子来量竿,却比竿尺;如果将绳索对半折后再去量竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果绳索对半折后再去量竿,就比竿短5尺.设绳索长 尺,竿长 尺,则符合题意的方程组是( )A、 B、 C、 D、8. 已知 是 的三边长,化简 的值是( )A、 B、 C、 D、9. 小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是( )A、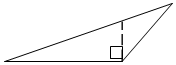 B、
B、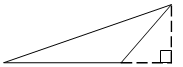 C、
C、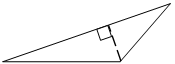 D、
D、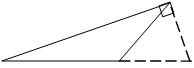 10. 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为 的新多边形,则原多边形的边数为( )
10. 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为 的新多边形,则原多边形的边数为( )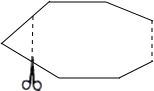 A、13 B、14 C、15 D、16
A、13 B、14 C、15 D、16二、填空题
-
11. 如果 满足 ,则 .12. 如图所示,已知点 分别是 的中点, 厘米2 , 则 平方厘米.
 13. 如图,在△ABC中,AB=AC=8,AB的垂直平分线DE分别交AB、AC于点E、 D,BD=BC,△BCD的周长为13,则BC和ED的长分别为.
13. 如图,在△ABC中,AB=AC=8,AB的垂直平分线DE分别交AB、AC于点E、 D,BD=BC,△BCD的周长为13,则BC和ED的长分别为.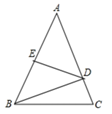 14. 下列说法:
14. 下列说法:
① 三角形的三条内角平分线都在三角形内,且相交于一点,正确;②在 中,若 ,则 一定是直角三角形;③三角形的一个外角大于任何一个内角;④若等腰三角形的两边长分别是3和5,则周长是13或11;⑤如果一个正多边形的每一个内角都比其外角多 ,那么该正多边形的边数是10,其中正确的说法有个.
15. 如图,把一副三角板如图甲放置,其中 ,斜边 ,把三角板 绕点 顺时针旋转 得到 (如图乙).这时 与 相交于点 , 与 相交于点 ,则 的度数为.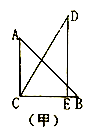
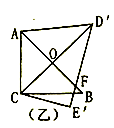
三、解答题
-
16.(1)、解方程组或不等式组
①解方程组
②解不等式组 把解集在数轴上表示出来,并写出不等式组的负整数解.
(2)、甲、乙两位同学一起解方程组 ,由于甲看错了方程①中的 ,得到的解为 ,乙看错了方程②中的 ,得到的解为 ,试计算的 值.17. 关于 的方程组 的解满足 ,求满足条件的整数 .18. 已知在图(1)与图(2)中,每个小方格都是边长为1个单位的正方形, 的三个顶点都在格点上.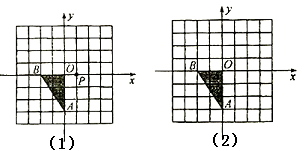 (1)、将 关于点 对称,在图(1)中画出对称后的图形 ,并涂黑;(2)、将△OAB先向右平移3个单位,再向上平移2个单位,在图2中画出平移后的图形,并涂黑。19. 如图, 是等边三角形, 旋转后能与 重合.
(1)、将 关于点 对称,在图(1)中画出对称后的图形 ,并涂黑;(2)、将△OAB先向右平移3个单位,再向上平移2个单位,在图2中画出平移后的图形,并涂黑。19. 如图, 是等边三角形, 旋转后能与 重合. (1)、旋转中心是哪一点?(2)、旋转角度是多少度?(3)、连结 后, 是什么三角形?简单说明理由.20. 在“国庆”黄金周期间,小明、小亮等同学随家人一同到某旅游区游玩.下图是购买门票时,小明与他爸爸的对话:
(1)、旋转中心是哪一点?(2)、旋转角度是多少度?(3)、连结 后, 是什么三角形?简单说明理由.20. 在“国庆”黄金周期间,小明、小亮等同学随家人一同到某旅游区游玩.下图是购买门票时,小明与他爸爸的对话:
问题:
(1)、小明他们一共去了几个成人?几个学生?(2)、用哪种方式买票更省钱?并说明理由;(3)、一位阿姨见小明这么聪明,也想考考他.她说:“我这里有大人,也有学生,学生人数比大人人数多,我们买票共花了105元,你能说出我们一共去了几个成人?几个学生?”聪明的你,请再帮小明算一算.21. 已知:如图, ,求 的度数.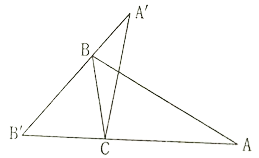 22. 为了争创全国文明卫生城市,优化城市环境,某市公交公司决定购买10辆全新的混合动力公交车,现有 两种型号,它们的价格及年省油量如下表:
22. 为了争创全国文明卫生城市,优化城市环境,某市公交公司决定购买10辆全新的混合动力公交车,现有 两种型号,它们的价格及年省油量如下表:型 号
价格(万元/辆)
年省油量(万升/辆)
2.4
2
经调查,购买一辆 型车比购买一辆 型车多20万元,购买2辆 型车比购买3辆 型车少60万元.
(1)、请求出 和 的值;(2)、若购买这批混合动力公交车(两种车型都要有), 每年能节省的油量不低于22.4万升,请问有几种购车方案?(不用一一列出)请求出最省钱的购车方案所需的车款.23. 如图,已知 ,点 分别在射线 上移动, 的平分线与 的外角平分线交于点 . (1)、当 时, .(2)、请你猜想:随着 两点的移动, 的度数大小是否变化?请说明理由.
(1)、当 时, .(2)、请你猜想:随着 两点的移动, 的度数大小是否变化?请说明理由.