甘肃省天水市2019年中考数学试卷
试卷更新日期:2019-07-22 类型:中考真卷
一、单选题
-
1. 已知 , 是2的相反数,则 的值为( )A、-3 B、-1 C、-1或-3 D、1或-32. 自然界中的数学不胜枚举,如蜜蜂建造的蜂房既坚固又省料,其厚度为0.000073米,将0.000073用科学记数法表示为(( )A、 B、 C、 D、3. 如图所示的圆锥的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 一把直尺和一块三角板 (含 、 角)如图所示摆放,直尺一边与三角板的两直角边分别交于点 和点 ,另一边与三角板的两直角边分别交于点 和点 ,且 ,那么 的大小为( )
4. 一把直尺和一块三角板 (含 、 角)如图所示摆放,直尺一边与三角板的两直角边分别交于点 和点 ,另一边与三角板的两直角边分别交于点 和点 ,且 ,那么 的大小为( )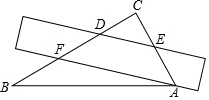 A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 已知 ,则代数式 的值是( )A、2 B、-2 C、-4 D、7. 如图,正方形 内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为( )
A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 已知 ,则代数式 的值是( )A、2 B、-2 C、-4 D、7. 如图,正方形 内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为( ) A、 B、 C、 D、8. 如图,等边 的边长为2,则点 的坐标为( )
A、 B、 C、 D、8. 如图,等边 的边长为2,则点 的坐标为( ) A、 B、 C、 D、9. 如图,四边形 是菱形, 经过点 、 、 ,与 相交于点 ,连接 、 .若 ,则 的度数为( )
A、 B、 C、 D、9. 如图,四边形 是菱形, 经过点 、 、 ,与 相交于点 ,连接 、 .若 ,则 的度数为( ) A、 B、 C、 D、10. 已知点 为某个封闭图形边界上一定点,动点 从点 出发,沿其边界顺时针匀速运动一周,设点 的运动时间为 ,线段 的长度为 ,表示 与 的函数图象大致如图所示,则该封闭图形可能是( )
A、 B、 C、 D、10. 已知点 为某个封闭图形边界上一定点,动点 从点 出发,沿其边界顺时针匀速运动一周,设点 的运动时间为 ,线段 的长度为 ,表示 与 的函数图象大致如图所示,则该封闭图形可能是( )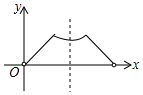 A、
A、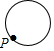 B、
B、 C、
C、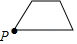 D、
D、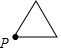
二、填空题
-
11. 函数y= 中,自变量x的取值范围是;实数2﹣ 的倒数是 .12. 分式方程 的解是.13. 一组数据2.2,3.3,4.4,11.1, .其中整数 是这组数据中的中位数,则这组数据的平均数是.14. 中国“一带一路”给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年人均年收入20000元,到2018年人均年收入达到39200元.则该地区居民年人均收入平均增长率为.(用百分数表示)15. 二次函数 的图象如图所示,若 , .则 、 的大小关系为 .(填“ ”、“ ”或“ ”)
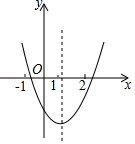 16. 如图,在平面直角坐标系中,已知 经过原点 ,与 轴、 轴分别交于 、 两点,点 坐标为 , 与 交于点 , ,则圆中阴影部分的面积为.
16. 如图,在平面直角坐标系中,已知 经过原点 ,与 轴、 轴分别交于 、 两点,点 坐标为 , 与 交于点 , ,则圆中阴影部分的面积为. 17. 如图,在矩形 中, , ,点 在 上,将矩形 沿 折叠,点 恰好落在 边上的点 处,那么 的值为.
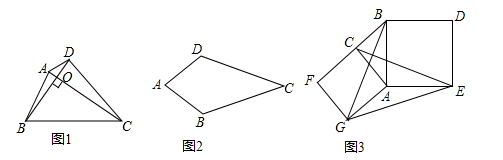
17. 如图,在矩形 中, , ,点 在 上,将矩形 沿 折叠,点 恰好落在 边上的点 处,那么 的值为.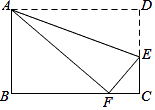 18. 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形中共有个〇.
18. 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形中共有个〇.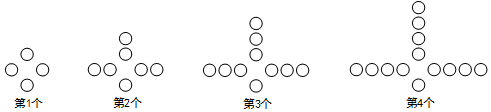
三、解答题
-
19.(1)、计算:(2)、先化简,再求值: ,其中 的值从不等式组 的整数解中选取.20. 天水市某中学为了解学校艺术社团活动的开展情况,在全校范围内随机抽取了部分学生,在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,围绕你最喜欢哪一项活动(每人只限一项)进行了问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
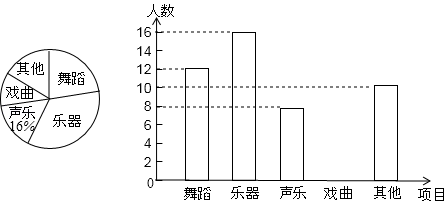
请你根据统计图解答下列问题:
(1)、在这次调查中,一共抽查了名学生.(2)、请你补全条形统计图.(3)、扇形统计图中喜欢“乐器”部分扇形的圆心角为度.(4)、请根据样本数据,估计该校1200名学生中喜欢“舞蹈”项目的共多少名学生?21. 如图,一次函数 与反比例函数 的图象交于 、 两点,与坐标轴分别交于 、 两点. (1)、求一次函数的解析式;(2)、根据图象直接写出 中 的取值范围;(3)、求 的面积.22. 某地的一座人行天桥如图所示,天桥高为6米,坡面 的坡度为 ,文化墙 在天桥底部正前方8米处( 的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为 .(参考数据: , )
(1)、求一次函数的解析式;(2)、根据图象直接写出 中 的取值范围;(3)、求 的面积.22. 某地的一座人行天桥如图所示,天桥高为6米,坡面 的坡度为 ,文化墙 在天桥底部正前方8米处( 的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为 .(参考数据: , )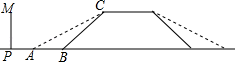 (1)、若新坡面坡角为 ,求坡角 度数;(2)、有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙 是否需要拆除?请说明理由.23. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.
(1)、若新坡面坡角为 ,求坡角 度数;(2)、有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙 是否需要拆除?请说明理由.23. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.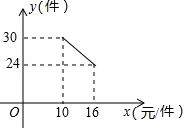 (1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?